题目内容
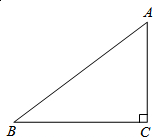 △ABC中,∠C=90°,AC=3,BC=4,在BC边上找一点P,使得点P到点C的距离与点P到边AB的距离相等.
△ABC中,∠C=90°,AC=3,BC=4,在BC边上找一点P,使得点P到点C的距离与点P到边AB的距离相等.(1)找出点P的位置(尺规作图).
(2)求BP的长.
考点:角平分线的性质,勾股定理,作图—基本作图
专题:
分析:(1)作∠CAB的平分线,交BC于点P,过点P作PD⊥AB于D,则PC=PD;
(2)先利用HL证明Rt△ADP≌Rt△ACP,得出AD=AC=3,再设PC=x,则PD=x,BP=4-x,在Rt△BDP中,由勾股定理得出(4-x)2=x2+22,解得:x=1.5,进而求出BP的值.
(2)先利用HL证明Rt△ADP≌Rt△ACP,得出AD=AC=3,再设PC=x,则PD=x,BP=4-x,在Rt△BDP中,由勾股定理得出(4-x)2=x2+22,解得:x=1.5,进而求出BP的值.
解答:解:(1)如图,点P即为所求;

(2)∵AP平分∠CAB,PD⊥AB于D,∠C=90°,
∴PD=PC.
在Rt△ADP和Rt△ACP中,
,
∴Rt△ADP≌Rt△ACP(HL),
∴AD=AC=3.
在Rt△ABC中,由勾股定理,得
AB=5,
∴BD=5-3=2.
设PC=x,则PD=x,BP=4-x,在Rt△BDP中,由勾股定理,得
(4-x)2=x2+22,
解得:x=1.5,
∴BP=4-1.5=2.5.
答:BP的长为2.5.

(2)∵AP平分∠CAB,PD⊥AB于D,∠C=90°,
∴PD=PC.
在Rt△ADP和Rt△ACP中,
|
∴Rt△ADP≌Rt△ACP(HL),
∴AD=AC=3.
在Rt△ABC中,由勾股定理,得
AB=5,
∴BD=5-3=2.
设PC=x,则PD=x,BP=4-x,在Rt△BDP中,由勾股定理,得
(4-x)2=x2+22,
解得:x=1.5,
∴BP=4-1.5=2.5.
答:BP的长为2.5.
点评:本题考查了勾股定理的运用,角平分线的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形的全等和运用勾股定理建立方程求解是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列分解因式正确的是( )
| A、-x2-y2=-(x+y)(x-y) |
| B、x2y+2xy+4y=y(x+2)2 |
| C、49x2-x2y2=(xy+7x)(xy-7x) |
| D、16x2+4y2-16xy=4(2x-y)2 |
若x=-6是关于x的方程
-(m-x)=1的解,则m的值为( )
| x |
| 3 |
| A、3 | B、9 | C、-9 | D、-3 |
 如图,长方形OABC中,OC=2,OA=1.以原点O为圆心,对角线OB长为半径画弧交数轴于点D,则数轴上点D表示的数是
如图,长方形OABC中,OC=2,OA=1.以原点O为圆心,对角线OB长为半径画弧交数轴于点D,则数轴上点D表示的数是 已知,如图,CD为Rt△ABC斜边AB上的高,∠BAC的平分线分别交CD、BC于E、F,FG⊥AB垂足为点G.求证:CE=FG.
已知,如图,CD为Rt△ABC斜边AB上的高,∠BAC的平分线分别交CD、BC于E、F,FG⊥AB垂足为点G.求证:CE=FG.