题目内容
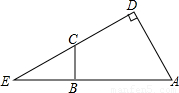
 如图,在△ADE中,∠D=90°,∠A=60°,点C是线段DE的中点,过C点作CB⊥AE于B,CB=2,求AB的长.
如图,在△ADE中,∠D=90°,∠A=60°,点C是线段DE的中点,过C点作CB⊥AE于B,CB=2,求AB的长.
分析:在△ADE中,根据三角形的内角和定理解得∠E=30°;然后,在Rt△CBE中,利用直角三角形的边角关系求得DE=8;最后,在Rt△ADE中,利用直角三角形中的边角关系sinA=
求得AE的值.所以AB=AE-BE就迎刃而解了.
| DE |
| AE |
解答:解:
解法一:
在△ADE中,∠D=90°,∠A=60°,
∴∠E=30°,
在Rt△CBE中,∠CBE=90°,∠E=30°,BC=2,
∴CE=4,BE=
=2
.(1分)
∵点C是线段DE的中点,
∴DE=8.(2分)
在Rt△ADE中,sinA=
∴AE=
=
=
(4分)
∴AB=AE-BE=
-2
=
.(5分)
解法二:
在△ADE中,∠D=90°,∠A=60°,∴∠E=30°
在Rt△CBE中,∠CBE=90°,∠E=30°,BC=2,
∴CE=4,BE=2
.(1分)
∵点C是线段DE的中点,
∴DE=8.(2分)
∵∠CBE=∠D=90°,∠E=∠E,
∴△CBE∽△ADE.(3分)
∴
=
即
=
∴AE=
.(4分)
∴AB=AE-BE=
-2
=
.(5分)
解法一:
在△ADE中,∠D=90°,∠A=60°,
∴∠E=30°,
在Rt△CBE中,∠CBE=90°,∠E=30°,BC=2,
∴CE=4,BE=
| 42-22 |
| 3 |
∵点C是线段DE的中点,
∴DE=8.(2分)
在Rt△ADE中,sinA=
| DE |
| AE |
∴AE=
| DE |
| sinA |
| 8 | ||||
|
16
| ||
| 3 |
∴AB=AE-BE=
16
| ||
| 3 |
| 3 |
10
| ||
| 3 |
解法二:
在△ADE中,∠D=90°,∠A=60°,∴∠E=30°
在Rt△CBE中,∠CBE=90°,∠E=30°,BC=2,
∴CE=4,BE=2
| 3 |
∵点C是线段DE的中点,
∴DE=8.(2分)
∵∠CBE=∠D=90°,∠E=∠E,
∴△CBE∽△ADE.(3分)
∴
| CE |
| AE |
| BE |
| DE |
即
| 4 |
| AE |
2
| ||
| 8 |
∴AE=
16
| ||
| 3 |
∴AB=AE-BE=
16
| ||
| 3 |
| 3 |
10
| ||
| 3 |
点评:解答本题时,主要利用了直角三角形中的边角关系.

练习册系列答案
相关题目
 10、如图,在△ABC中,D,E分别是AB,AC的中点,那么△ADE与四边形DBCE的面积之比是
10、如图,在△ABC中,D,E分别是AB,AC的中点,那么△ADE与四边形DBCE的面积之比是 如图,在△ABC中,若AD•AB=AE•AC;求证:∠ADE=∠C.
如图,在△ABC中,若AD•AB=AE•AC;求证:∠ADE=∠C.