题目内容
20. 如图,AB是⊙O的直径,C为⊙O上一点,PC切⊙O于C,AE⊥PC交PC的延长线于E,AE交⊙O于D,PC与AB的延长线相交于点P,连接AC、BC.
如图,AB是⊙O的直径,C为⊙O上一点,PC切⊙O于C,AE⊥PC交PC的延长线于E,AE交⊙O于D,PC与AB的延长线相交于点P,连接AC、BC.(1)求证:AC平分∠BAD;
(2)若PB:PC=1:2,PB=4,求AB的长.
分析 (1)先AE∥OC,然后依据平行线的性质可得到∠EAC=∠ACO.,接下来由∠ACO=∠AOC,可证明∠EAC=∠OAC;
(2)先证明∠PCB=∠PAC,从而可证明△PCA∽△PBC,依据相似三角形的性质可求得PA的长,最后依据AB=PA-PB求解即可.
解答 解:(1)如图所示:连结OC.
∵PC是⊙O的切线,
∴OC⊥EP.
又∵AE⊥PC,
∴AE∥OC.
∴∠EAC=∠ACO.
又∵∠ACO=∠AOC,
∴∠EAC=∠OAC.
∴AC平分∠BAD;
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC+∠ABC=90°.
∵OB=OC,
∴∠OCB=∠ABC.
∵∠PCB+∠OCB=90°,
∴∠PCB=∠PAC.
∵∠P=∠P,
∴△PCA∽△PBC,
∴$\frac{PC}{PB}$=$\frac{PA}{PC}$,
∴PA=$\frac{P{C}^{2}}{PB}$=16.
∴AB=PA-PB=16-4=12.
点评 本题主要考查的是相似三角形的性质和判定、切线的性质、圆周角定理的应用,熟练掌握相关定理是解题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
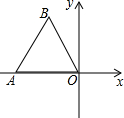 如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,则点A′的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,则点A′的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
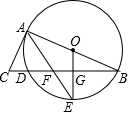 如图,AB是⊙O的直径,BC交⊙O于点D,E是BD弧上的一点,OE⊥BD于点G,连接AE交BC于点F,AC是⊙O的切线.
如图,AB是⊙O的直径,BC交⊙O于点D,E是BD弧上的一点,OE⊥BD于点G,连接AE交BC于点F,AC是⊙O的切线.
 已知:如图,∠C=∠EDB,∠2=∠3,求证:∠B=∠FDC.
已知:如图,∠C=∠EDB,∠2=∠3,求证:∠B=∠FDC.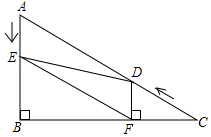 如图,在Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.