题目内容
 (1)这圆锥侧面展开的圆心角为n°,母线长为R,底面半径为r,填表:
(1)这圆锥侧面展开的圆心角为n°,母线长为R,底面半径为r,填表:| n | 60° | 72° | 90° | 120° |
| R与r之间的函数解析式 |
考点:圆锥的计算,相切两圆的性质
专题:计算题
分析:(1)利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2π•r=
,即R=
,然后把n=60°、72°、90°、120°分别代入计算即可得到R与r的关系;
(2)由(1)得R=4r,
如图1,根据正方形的性质得AD=20
,根据圆的切线的性质和圆与圆相切的性质易得AD=AB+BC+CD=R+r+
r,则4r+r+
r=20
,解得r≈4.4(cm),再计算出R,然后利用勾股定理计算圆锥的高.
| n•π•R |
| 180 |
| 360 |
| n |
(2)由(1)得R=4r,
如图1,根据正方形的性质得AD=20
| 2 |
| 2 |
| 2 |
| 2 |
解答: 解:(1)∵2π•r=
解:(1)∵2π•r=
,
∴R=
当n=60°时,R=6r;当n=72°时,R=5r;当n=90°时,R=4r;当n=120°时,R=3r;
故答案为R=6r,R=5r,R=4r,R=3r;
(2)由(1)得R=4r,
如图1,AD=20
,
∵AD=AB+BC+CD=R+r+
r,
∴4r+r+
r=20
,解得r≈4.4(cm);
∴R=4r=17.6cm,
∴圆锥的高=
≈17.1(cm).
故答案为4.4,17.6.
 解:(1)∵2π•r=
解:(1)∵2π•r=| n•π•R |
| 180 |
∴R=
| 360 |
| n |
当n=60°时,R=6r;当n=72°时,R=5r;当n=90°时,R=4r;当n=120°时,R=3r;
故答案为R=6r,R=5r,R=4r,R=3r;
(2)由(1)得R=4r,
如图1,AD=20
| 2 |
∵AD=AB+BC+CD=R+r+
| 2 |
∴4r+r+
| 2 |
| 2 |
∴R=4r=17.6cm,
∴圆锥的高=
| 17.62-4.42 |
故答案为4.4,17.6.
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了两圆相切的性质和等腰直角三角形的性质.

练习册系列答案
相关题目
若a+b=0,ab=-11,那么a2-ab+b2的值为( )
| A、11 | B、-11 |
| C、-33 | D、33 |
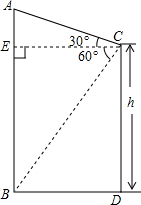 在一个高为h的楼顶上,测的远处一个建筑物AB的顶部与底部的仰角与俯角分别为30°和60°,用h表示这个建筑物的高度.
在一个高为h的楼顶上,测的远处一个建筑物AB的顶部与底部的仰角与俯角分别为30°和60°,用h表示这个建筑物的高度.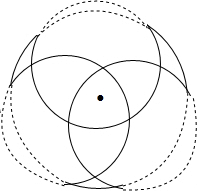 观察图中由粗线条勾勒出来的图形,犹如“三鱼戏水”,试模仿此图再画一个“三鱼戏水”图,体会圆与圆的位置关系,你还能利用圆与圆、圆与正多边形的位置关系,画出一个或几个有特色的图案吗?
观察图中由粗线条勾勒出来的图形,犹如“三鱼戏水”,试模仿此图再画一个“三鱼戏水”图,体会圆与圆的位置关系,你还能利用圆与圆、圆与正多边形的位置关系,画出一个或几个有特色的图案吗? 如图,PE⊥AB于E,F在CD上,∠EPF=130°,∠PFC=40°,那么AB∥CD;
如图,PE⊥AB于E,F在CD上,∠EPF=130°,∠PFC=40°,那么AB∥CD; 如图,∠A+∠B=180°,∠EFC=∠DCG,试说明:AD∥EF.
如图,∠A+∠B=180°,∠EFC=∠DCG,试说明:AD∥EF.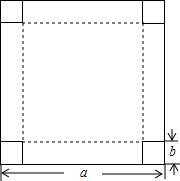 在一块边长为a厘米的正方形纸板四角,各剪去一个边长为b(b<
在一块边长为a厘米的正方形纸板四角,各剪去一个边长为b(b< 如图,长和宽分别是a,b的长方形纸片的四个角都剪去一个边长为x的正方形.
如图,长和宽分别是a,b的长方形纸片的四个角都剪去一个边长为x的正方形.