题目内容
 如图,梯形ABCD是直角梯形,对角线AC将其分成两部分,如果△ACD是正三角形且面积为
如图,梯形ABCD是直角梯形,对角线AC将其分成两部分,如果△ACD是正三角形且面积为 ,那么△ABC的面积为________.
,那么△ABC的面积为________.
2
分析:首先过点A作AE⊥CD于点E,易得四边形ABCE是矩形,又由△ACD是正三角形且面积为 ,可求得AE与CD的长,继而可得AD与BC的长,则可求得△ABC的面积.
,可求得AE与CD的长,继而可得AD与BC的长,则可求得△ABC的面积.
解答: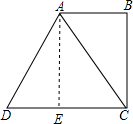 解:过点A作AE⊥CD于点E,
解:过点A作AE⊥CD于点E,
∵梯形ABCD是直角梯形,AB∥CD,
∴四边形ABCE是矩形,
∴AD=CE,AE=BC,
∵△ACD是正三角形,
∴CE= CD,AE=
CD,AE= CD,
CD,
∵△ACD的面积为 ,
,
即 CD•AE=4
CD•AE=4 ,
,
解得:CD=4,
∴CE=2,BC=AE=2 ,
,
∴△ABC的面积为: AB•BC=
AB•BC= ×2×2
×2×2 =2
=2 .
.
故答案为:2 .
.
点评:此题考查了直角梯形的性质、矩形的判定与性质以及等边三角形的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

分析:首先过点A作AE⊥CD于点E,易得四边形ABCE是矩形,又由△ACD是正三角形且面积为
 ,可求得AE与CD的长,继而可得AD与BC的长,则可求得△ABC的面积.
,可求得AE与CD的长,继而可得AD与BC的长,则可求得△ABC的面积.解答:
 解:过点A作AE⊥CD于点E,
解:过点A作AE⊥CD于点E,∵梯形ABCD是直角梯形,AB∥CD,
∴四边形ABCE是矩形,
∴AD=CE,AE=BC,
∵△ACD是正三角形,
∴CE=
 CD,AE=
CD,AE= CD,
CD,∵△ACD的面积为
 ,
,即
 CD•AE=4
CD•AE=4 ,
,解得:CD=4,
∴CE=2,BC=AE=2
 ,
,∴△ABC的面积为:
 AB•BC=
AB•BC= ×2×2
×2×2 =2
=2 .
.故答案为:2
 .
.点评:此题考查了直角梯形的性质、矩形的判定与性质以及等边三角形的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
 如图等腰梯形ABCD是⊙O的外切四边形,O是圆心,腰长4cm,则∠BOC=
如图等腰梯形ABCD是⊙O的外切四边形,O是圆心,腰长4cm,则∠BOC=
 (2012•凉山州)如图,梯形ABCD是直角梯形.
(2012•凉山州)如图,梯形ABCD是直角梯形.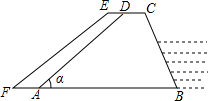 (2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.
(2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米. 费用为0.05万元/m2,若设计要求通道宽度x≤8m,则宽度x为多少时,世纪广场修建总费用最少?最少费用为多少?
费用为0.05万元/m2,若设计要求通道宽度x≤8m,则宽度x为多少时,世纪广场修建总费用最少?最少费用为多少?