题目内容
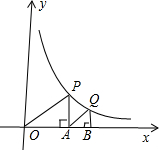
 如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=
如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=| 4 | x |
分析:由△OAP是等腰直角三角形可以得到PA=OA,可以设P点的坐标是(a,a),把(a,a)代入反比例函数解析式即可求出a=1,然后求出P的坐标,从而求出OA,再根据△ABQ是等腰直角三角形用同样的方法即可求出点B的坐标.
解答:解:∵△OAP是等腰直角三角形,
∴PA=OA,
∴设P点的坐标是(a,a),
把(a,a)代入解析式得到a=2,
∴P的坐标是(2,2),
∴OA=2,
∵△ABQ是等腰直角三角形,
∴BQ=AB,
∴可以设Q的纵坐标是b,
∴横坐标是b+2,
把Q的坐标代入解析式y=
,
得到b=
,
∴b=-1+
,(b=-1-
舍去)
∴点B的坐标为(
+1,0).
故答案为:(
+1,0).
∴PA=OA,
∴设P点的坐标是(a,a),
把(a,a)代入解析式得到a=2,
∴P的坐标是(2,2),
∴OA=2,
∵△ABQ是等腰直角三角形,
∴BQ=AB,
∴可以设Q的纵坐标是b,
∴横坐标是b+2,
把Q的坐标代入解析式y=
| 4 |
| x |
得到b=
| 4 |
| b+2 |
∴b=-1+
| 5 |
| 5 |
∴点B的坐标为(
| 5 |
故答案为:(
| 5 |
点评:本题考查了反比例函数的图象的性质以及等腰直角三角形的性质,利用形数结合解决此类问题,是非常有效的方法.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 如图,△OAP、△ABQ均是直角三角形,且∠POA=∠QAB=30°,点P、Q在函数y=
如图,△OAP、△ABQ均是直角三角形,且∠POA=∠QAB=30°,点P、Q在函数y= 如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=
如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y= 、B均在x轴上,已知OP=
、B均在x轴上,已知OP=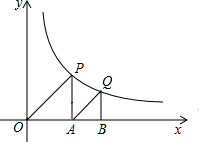 、B均在x轴上,已知OP=
、B均在x轴上,已知OP= .
.