题目内容
 如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=
如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=| 4 | x |
分析:若△OAP是等腰直角三角形,那么∠POA=45°,即直线OP:y=x,联立双曲线解析式可求得P(2,2),即A(2,0),然后结合直线OP的斜率求得直线AQ的解析式,联立反比例函数解析式即可得到点Q点坐标,由于B、Q的横坐标相同,即可得解.
解答:解:∵△OAP是等腰直角三角形,
∴直线OP:y=x,联立y=
(x>0)可得P(2,2);
∴A(2,0),
由于直线OP∥AQ,可设直线AQ:y=x+h,则有:
2+h=0,h=-2;
∴直线AQ:y=x-2;
联立y=
(x>0)可得Q(1+
,
-1),即B(1+
,0).
故答案为:(1+
,0).
∴直线OP:y=x,联立y=
| 4 |
| x |

∴A(2,0),
由于直线OP∥AQ,可设直线AQ:y=x+h,则有:
2+h=0,h=-2;
∴直线AQ:y=x-2;
联立y=
| 4 |
| x |
| 5 |
| 5 |
| 5 |
故答案为:(1+
| 5 |
点评:此题主要考查了等腰直角三角形的性质以及函数图象交点坐标的求法,难度适中.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
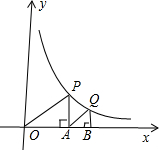 如图,△OAP、△ABQ均是直角三角形,且∠POA=∠QAB=30°,点P、Q在函数y=
如图,△OAP、△ABQ均是直角三角形,且∠POA=∠QAB=30°,点P、Q在函数y= 如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数
如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数 、B均在x轴上,已知OP=
、B均在x轴上,已知OP=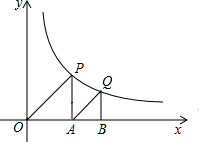 、B均在x轴上,已知OP=
、B均在x轴上,已知OP= .
.