题目内容
 如图,梯形ABCD中,AB∥CD,点M、N分别是AD、BC的中点,DE⊥AB,垂足为点E.若四边形BCDE是正方形,且点M、N关于直线DE对称,则∠DAE的余切值为________.
如图,梯形ABCD中,AB∥CD,点M、N分别是AD、BC的中点,DE⊥AB,垂足为点E.若四边形BCDE是正方形,且点M、N关于直线DE对称,则∠DAE的余切值为________.
2
分析:根据正方形的性质以及三角形的中位线性质得出EF= AE,进而得出MF=FN=DE,即可得出答案.
AE,进而得出MF=FN=DE,即可得出答案.
解答:连接MN,
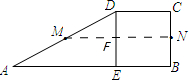 ∵AB∥CD,点M、N分别是AD、BC的中点,
∵AB∥CD,点M、N分别是AD、BC的中点,
∴EF= AE,
AE,
∵四边形BCDE是正方形,且点M、N关于直线DE对称,
∴MF=FN=DE,
cot∠DAE=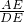 =
= =2.
=2.
故答案为:2.
点评:此题主要考查了锐角三角函数的定义以及正方形的性质和三角形中位线性质等知识,根据题意得出MF=FN=DE是解决问题的关键.
分析:根据正方形的性质以及三角形的中位线性质得出EF=
 AE,进而得出MF=FN=DE,即可得出答案.
AE,进而得出MF=FN=DE,即可得出答案.解答:连接MN,
 ∵AB∥CD,点M、N分别是AD、BC的中点,
∵AB∥CD,点M、N分别是AD、BC的中点,∴EF=
 AE,
AE,∵四边形BCDE是正方形,且点M、N关于直线DE对称,
∴MF=FN=DE,
cot∠DAE=
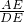 =
= =2.
=2.故答案为:2.
点评:此题主要考查了锐角三角函数的定义以及正方形的性质和三角形中位线性质等知识,根据题意得出MF=FN=DE是解决问题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2, 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.