题目内容
16.已知二次函数y=ax2+bx+c,当x=1时,y=2;当x=-1时,y=4;当x=0时,y=0.则这个二次函数的表达式为y=3x2-x.分析 将x=1、y=2;x=-1、y=4;x=0、y=0代入y=ax2+bx+c得出关于a、b、c的方程组,解方程组即可得.
解答 解:将x=1、y=2;x=-1、y=4;x=0、y=0代入y=ax2+bx+c,
得:$\left\{\begin{array}{l}{a+b+c=2}\\{a-b+c=4}\\{c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=3}\\{b=-1}\\{c=0}\end{array}\right.$,
∴这个二次函数的表达式为y=3x2-x,
故答案为:y=3x2-x.
点评 本题主要考查待定系数法求二次函数的解析式,在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
6.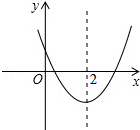 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:
①a>0;②b<0;③b<a+c;④4a+2b+c>0其中正确结论的有( )
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①a>0;②b<0;③b<a+c;④4a+2b+c>0其中正确结论的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
7.要使式子$\frac{\sqrt{a-2}}{a-3}$有意义,a的取值范围是( )
| A. | a≠3 | B. | a>2且a≠3 | C. | a≥2或a≠3 | D. | a≥2且a≠3 |
4.福州地铁规划总长约180000米,用科学记数法表示这个总长为( )
| A. | 0.18×106米 | B. | 1.8×106米 | C. | 1.8×105米 | D. | 18×104米 |
1.下列算式能用平方差公式计算的是( )
| A. | (2a+b)(2b-a) | B. | (-2x-1)(-2x-1) | C. | (3x-y)(-3x+y) | D. | (-m-n)(-m+n) |
6.下列式子:①-2<0;②2x-3y<0;③x=3;④x+y.其中不等式的个数有( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |