题目内容
6.化简求值:(1-$\frac{1}{a-1}$)÷($\frac{{a}^{2}-4a+4}{{a}^{2}-a}$),其中a=$\sqrt{3}$+2.分析 根据分式的减法和除法可以化简题目中的式子,再将a的值代入化简后的式子即可解答本题.
解答 解:(1-$\frac{1}{a-1}$)÷($\frac{{a}^{2}-4a+4}{{a}^{2}-a}$)
=$\frac{a-1-1}{a-1}÷\frac{(a-2)^{2}}{a(a-1)}$
=$\frac{a-2}{a-1}•\frac{a(a-1)}{(a-2)^{2}}$
=$\frac{a}{a-2}$,
当a=$\sqrt{3}$+2时,原式=$\frac{\sqrt{3}+2}{\sqrt{3}+2-2}=\frac{\sqrt{3}+2}{\sqrt{3}}=\frac{3+2\sqrt{3}}{3}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
14. 如图,直线a、b被直线c所截,互为同旁内角是( )
如图,直线a、b被直线c所截,互为同旁内角是( )
 如图,直线a、b被直线c所截,互为同旁内角是( )
如图,直线a、b被直线c所截,互为同旁内角是( )| A. | ∠4和∠6 | B. | ∠2和∠7 | C. | ∠4和∠5 | D. | ∠4和∠6 |
17.在下列图形中,是中心对称图形而不是轴对称图形的是( )
| A. | 圆 | B. | 等边三角形 | C. | 梯形 | D. | 平行四边形 |
11.如果a>b、c<0,那么下列不等式成立的是( )
| A. | c-a>c-b | B. | a+c>b+c | C. | ac>bc | D. | $\frac{a}{c}$>$\frac{b}{c}$ |
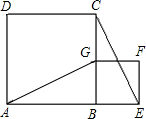 如图,正方形BEFG的边BG在正方形ABCD的边BC上,连结AG,EC.
如图,正方形BEFG的边BG在正方形ABCD的边BC上,连结AG,EC.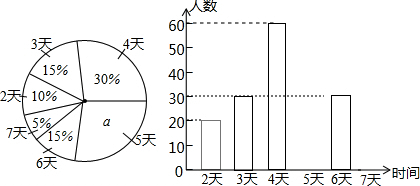
 如图所示,表示一人骑自行车和一人骑摩托车沿相同路线由甲地到乙地行驶过程中路程随时间变化的图象.两地间的距离是80千米,请你根据图象回答问题:
如图所示,表示一人骑自行车和一人骑摩托车沿相同路线由甲地到乙地行驶过程中路程随时间变化的图象.两地间的距离是80千米,请你根据图象回答问题: