题目内容
4.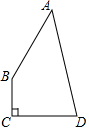 四边形ABCD中,AB=12,BC=3,CD=4,AD=13,且∠C=90°,则四边形ABCD的面积为( )
四边形ABCD中,AB=12,BC=3,CD=4,AD=13,且∠C=90°,则四边形ABCD的面积为( )| A. | 84 | B. | 36 | C. | 54 | D. | 72 |
分析 连接BD,知四边形的面积是△ADB和△BCD的面积和,由已知得其符合勾股定理的逆定理从而得到△ABD是一个直角三角形,则四边形面积可求.
解答  解:连接BD,
解:连接BD,
在Rt△BCD中,∠C=90°,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=5,
∵52+122=132,
即BD2+AB2=AD2,
∴△ABD为直角三角形,
∴四边形的面积=S△ADB+S△BCD=$\frac{1}{2}$BD•AB+$\frac{1}{2}$BC•CD=$\frac{1}{2}$×5×12+$\frac{1}{2}$×3×4=36.
故选:B.
点评 考查了勾股定理和它的逆定理,本题利用了勾股定理和它的逆定理及直角三角形的面积公式求解.隐含了整体的数学思想和正确运算的能力.

练习册系列答案
相关题目
19.若长方形的长为2a+1,宽为3a2-2a+1,则这个长方形的面积是( )
| A. | 6a3+2a2+1 | B. | 6a3-a2+1 | C. | 6a3+1 | D. | 6a3-1 |
 水果市场中的甲、乙两家商店中都批发同一种水果,批发水果x千克时,在甲、乙两家商店的批发价分别为y1元和y2元,已知y1和y2关于x的函数图象分别为如图所示的折线OAB和射线OC.
水果市场中的甲、乙两家商店中都批发同一种水果,批发水果x千克时,在甲、乙两家商店的批发价分别为y1元和y2元,已知y1和y2关于x的函数图象分别为如图所示的折线OAB和射线OC. 的解集是( )
的解集是( ) B、
B、 C、
C、 D、
D、
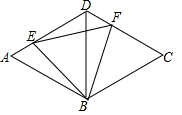 如图,在边长为4的菱形ABCD中,BD=4,E、F分别是边AD、CD上的动点,且AE+CF=4,连接BE、EF、FB.
如图,在边长为4的菱形ABCD中,BD=4,E、F分别是边AD、CD上的动点,且AE+CF=4,连接BE、EF、FB. 如图,若∠ADE=∠ABC,则DE∥BC,理由:同位角相等,两直线平行.
如图,若∠ADE=∠ABC,则DE∥BC,理由:同位角相等,两直线平行.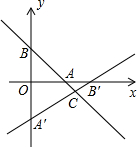 如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴,y轴于点A,B,直线A′B′分别交x轴,y轴于点B′,A′,且△AOB≌△A′OB′.
如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴,y轴于点A,B,直线A′B′分别交x轴,y轴于点B′,A′,且△AOB≌△A′OB′.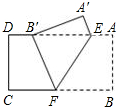 如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,若AE=3,AB=4,∠EFB=60°,则四边形A′B′FE的周长是=17.
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,若AE=3,AB=4,∠EFB=60°,则四边形A′B′FE的周长是=17.