题目内容
15.若实数x,y满足(x-$\sqrt{{x}^{2}-2016}$)(y-$\sqrt{{y}^{2}-2016}$)=2016.(1)求x,y之间的数量关系;
(2)求3x2-2y2+3x-3y-2017的值.
分析 (1)将式子变形后,再分母有理化得①式:x-$\sqrt{{x}^{2}-2016}$=y+$\sqrt{{y}^{2}-2016}$,同理得②式:x+$\sqrt{{x}^{2}-2016}$=y-$\sqrt{{y}^{2}-2016}$,将两式相加可得结论;
(2)将x=y代入原式或①式得:x2=2016,代入所求式子即可.
解答 解:(1)∵(x-$\sqrt{{x}^{2}-2016}$)(y-$\sqrt{{y}^{2}-2016}$)=2016,
∴x-$\sqrt{{x}^{2}-2016}$=$\frac{2016}{y-\sqrt{{y}^{2}-2016}}$=$\frac{2016(y+\sqrt{{y}^{2}-2016})}{{y}^{2}-({y}^{2}-2016)}$=y+$\sqrt{{y}^{2}-2016}$①,
同理得:x+$\sqrt{{x}^{2}-2016}$=y-$\sqrt{{y}^{2}-2016}$②,
①+②得:2x=2y,
∴x=y,
(2)把x=y代入①得:x-$\sqrt{{x}^{2}-2016}$=x+$\sqrt{{x}^{2}-2016}$,
x2=2016,
则3x2-2y2+3x-3y-2017,
=3x2-2x2+3x-3x-2017,
=x2-2017,
=2016-2017,
=-1.
点评 本题是二次根式的化简和求值,有难度,考查了二次根式的性质和分母有理化;二次根式中分母中含有根式时常运用分母有理化来解决,分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式.本题利用巧解将已知式变成两式,相加后得出结论.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
7.若关于x的方程$\frac{3}{x-3}$=$\frac{2}{k-3}$有正根,则k的取值范围是( )
| A. | k>1 | B. | k>3 | C. | k≠3 | D. | k>1且k≠3 |
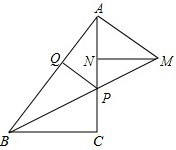 如图,已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN,NP=2,PC=3.
如图,已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN,NP=2,PC=3.