Question

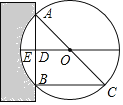
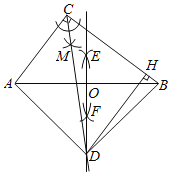
【题目】如图所示，是小聪同学在一次数学兴趣小组活动中，用直尺和圆规对Rt△ACB（∠ACB=90°）进行了如下操作：

①作边AB的垂直平分线EF交AB于点O；

②作∠ACB的平分线CM，CMEF相交于点D；

③连接AD，BD．

请你根据操作，观察图形解答下列问题：

（1）△ABD的形状是______；

（2）若DH⊥BC于点H，已知AC=6，BC=8，求BH的长．

Answer 1

【答案】（1）△ABD的形状是：等腰直角三角形．（2）1

【解析】

（1）根据作图可知△ABD的形状是：等腰直角三角形．

（2）过点D作DG⊥CA交CA的延长线于点G，证明四边形DHCG是正方形，Rt△ADG≌Rt△BDH（HL）即可解决问题．

解：（1）△ABD的形状是：等腰直角三角形．（理由见（2）中证明）．

故答案为：等腰直角三角形．

（2）过点D作DG⊥CA交CA的延长线于点G，

∵CM平分∠ACB，DH⊥BC，

∴DG=DH，

∵∠ACB=90°，

∴四边形DHCG是正方形，

∴CG=CH，

∵EF垂直平分AB

∴AD=BD

在Rt△ADG和Rt△BDH中，

，

∴Rt△ADG≌Rt△BDH（HL），

∴AG=BH，∠ADG=∠BDH，

∴∠ADB=∠GDH=90°，

∴△ADB是等腰直角三角形，

∴BC-AC=（CH+BH）-（CG-AG）=2BH，

∴BH= ．

故答案为：（1）△ABD的形状是：等腰直角三角形．（2）1．