Question

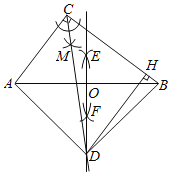
【题目】定义：如图，在△ABC中，∠C＝30°，我们把∠A的对边与∠C 的对边的比叫做∠A的邻弦，记作thi A，即thi A＝＝ ．请解答下列问题：

已知：在△ABC中，∠C＝30°．

（1）若∠A＝45°，求thi A的值；

（2）若thi A＝，则∠A＝ °；

（3）若∠A是锐角，探究thi A与sinA的数量关系．

Answer 1

【答案】（1）thiA＝；

（2）60或120；

（3）thiA＝2sinA

【解析】

试题(1) 根据已知找到BC和AB的关系，依据定义计算出答案即可；

(2) 过点B向AC所在直线作垂线，根据thi A＝=，利用正弦首先表示出垂线段的长度，再根据正弦分两种情况：当∠A为锐角或钝角时，可得∠A=60°或120°.

(3) 根据题意，由thiA＝, sinA＝, sinC＝＝易得BC＝2BH，进而可得答案．

试题解析：

解：（1）如图，作BH⊥AC，垂足为H．

在Rt△BHC中，sinC＝＝，即BC＝2BH．

在Rt△BHA中，sinA＝＝ ，即AB＝BH．

∴thiA＝＝．

（2）60或120．

（3）在Rt△ABC中，thiA＝．

在Rt△BHA中，sinA＝．

在Rt△BHC中，sinC＝＝，即BC＝2BH．

∴thiA＝2sinA．