题目内容
如图，在▱ABCD中，DE⊥AB，BF⊥CD，垂足分别为E，F．
（1）求证：△ADE≌△CBF；
（2）求证：四边形BFDE为矩形．
证明：（1）∵DE⊥AB，BF⊥CD，
∴∠AED=∠CFB=90°，
∵四边形ABCD为平行四边形，
∴AD=BC，∠A=∠C，
在△ADE和△CBF中，
，
∴△ADE≌△CBF（AAS）；
（2）∵四边形ABCD为平行四边形，
∴CD∥AB，
∴∠CDE+∠DEB=180°，
∵∠DEB=90°，
∴∠CDE=90°，
∴∠CDE=∠DEB=∠BFD=90°，
则四边形BFDE为矩形．
练习册系列答案
百年学典课时学练测系列答案
相关题目
﹣2）0+（
）﹣1+4cos30°﹣|
|
+
=
C． （x﹣3）2=x2﹣9 D． （x2）3=x6
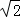个单位/秒的速度匀速运动，连接PQ，设运动时间为t秒．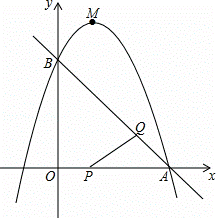
= _______
