��Ŀ����
��ͼ����ֱ֪��y=﹣x+3��x�ᡢy��ֱ���A��B���㣬������y=﹣x2+bx+c����A��B���㣬��P���߶�OA�ϣ��ӵ�O���������A��1����λ/����ٶ������˶���ͬʱ����Q���߶�AB�ϣ��ӵ�A���������B��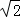 ����λ/����ٶ������˶�������PQ�����˶�ʱ��Ϊt�룮
����λ/����ٶ������˶�������PQ�����˶�ʱ��Ϊt�룮
��1���������ߵĽ���ʽ��
��2���ʣ���tΪ��ֵʱ����APQΪֱ�������Σ�
��3������P��PE��y�ᣬ��AB�ڵ�E������Q��QF��y�ᣬ���������ڵ�F������EF����EF��PQʱ�����F�����ꣻ
��4���������߶���ΪM������BP��BM��MQ���ʣ��Ƿ����t��ֵ��ʹ��B��Q��MΪ���������������O��B��PΪ��������������ƣ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
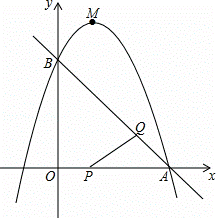
�⣺��1����y=﹣x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��
�൱y=0ʱ��x=3����A������Ϊ��3��0����
��x=0ʱ��y=3����B������Ϊ��0��3����
��A��3��0����B��0��3������y=﹣x2+bx+c��
�� �����
�����
�������ߵĽ���ʽΪy=﹣x2+2x+3��
��2����OA=OB=3����BOA=90�㣬
���QAP=45�㣮

��ͼ����ʾ����PQA=90��ʱ�����˶�ʱ��Ϊt�룬��QA= ��PA=3﹣t��
��PA=3﹣t��
��Rt��PQA�� ������
������ ����ã�t=1��
����ã�t=1��
��ͼ����ʾ����QPA=90��ʱ�����˶�ʱ��Ϊt�룬��QA= ��PA=3﹣t��
��PA=3﹣t��
��Rt��PQA�� ������
������ ����ã�t=
����ã�t= ��
��
������������t=1��t= ʱ����PQA��ֱ�������Σ�
ʱ����PQA��ֱ�������Σ�
��3����ͼ����ʾ��

���P������Ϊ��t��0�������E������Ϊ��t��﹣t+3������EP=3﹣t����Q������Ϊ��3﹣t��t������F������Ϊ��3﹣t��﹣��3﹣t��2+2��3﹣t��+3������FQ=3t﹣t2��
��EP��FQ��EF��PQ��
��EP=FQ������3﹣t=3t﹣t2��
��ã�t1=1��t2=3����ȥ����
��t=1����F��3﹣t��﹣��3﹣t��2+2��3﹣t��+3�����õ�F������Ϊ��2��3����
��4����ͼ����ʾ��

���˶�ʱ��Ϊt�룬��OP=t��BQ=��3﹣t�� ��
��
��y=﹣x2+2x+3=﹣��x﹣1��2+4��
���M��������1��4����
��MB= =
= ��
��
����BOP�ס�QBMʱ�� ����
���� �������ã�t2﹣3t+3=0��
�������ã�t2﹣3t+3=0��
��=32﹣4��1��3��0���⣺
����BOP�ס�MBQʱ�� ����
���� �����t=
�����t= ��
��
�൱t= ʱ����B��Q��MΪ���������������O��B��PΪ��������������ƣ�
ʱ����B��Q��MΪ���������������O��B��PΪ��������������ƣ�

 +
+ �Ľ����ȷ��0.01Ϊ�����ü������������㣩��������
�Ľ����ȷ��0.01Ϊ�����ü������������㣩��������
 ���У���ô�������еĸ߶�
���У���ô�������еĸ߶� ��ʱ��
��ʱ�� �仯��ͼ������ǣ� ��
�仯��ͼ������ǣ� ��
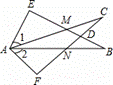
 ��ͼ��λ��ƽ��ֱ������ϵ�ģ�������
��ͼ��λ��ƽ��ֱ������ϵ�ģ������� �� ��һ�������� B�� �ڶ��������� C�� ��һ�������� D�� ������������
�� ��һ�������� B�� �ڶ��������� C�� ��һ�������� D�� ������������