Question

如图1，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．

（1）①找出图1中的一对全等三角形并说明理由；

②写出图1中线段DE、AD、BE满足的数量关系;（不必说明理由）

（2）当直线MN绕点C旋转到图2的位置时, 探究线段DE、AD、BE之间的数量关系并说明理由；

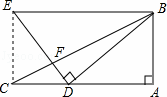
（3）当直线MN绕点C旋转到图3的位置时,问DE、AD、BE之间又具有怎样的数量关系？直接写出这个数量关系（不必说明理由）．

 

 

 

Answer 1

解：（1）①△ADC≌△CEB．

理由如下：：∵∠ACB=90°，∠ADC=90°，∠BEC=90°

∴∠ACD+∠DAC=90°，∠ACD+∠BCE=90°，

∴∠DAC=∠BCE，

在△ADC与△BEC中，，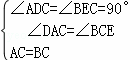

∴△ADC≌△BEC（AAS）；

 

②DE=CE+CD=AD+BE．

理由如下：

由①知，△ADC≌△BEC，

∴AD=CE，BE=CD，

∵DE=CE+CD，

∴DE=AD+BE；

 

 

（2）∵AD⊥MN于D，BE⊥MN于E．

∴∠ADC=∠BEC=∠ACB=90°，

∴∠CAD+∠ACD=90°，∠ACD+∠BCE=90°．

∴∠CAD=∠BCE．

在△ADC和△CEB中，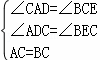

∴△ADC≌△CEB．

∴CE=AD，CD=BE．

∴DE=CE﹣CD=AD﹣BE．

 

（3）同（2），易证△ADC≌△CEB．

∴AD=CE，BE=CD

∵CE=CD﹣ED

∴AD=BE﹣ED，即ED=BE﹣AD；

当MN旋转到图3的位置时，AD、DE、BE所满足的等量关系是DE=BE﹣AD（或AD=BE﹣DE，BE=AD+DE等）．