题目内容
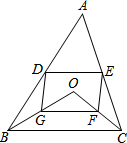 如图,D、E分别是△ABC的边AB、AC的中点,点O是△ABC内部任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是△ABC的边AB、AC的中点,点O是△ABC内部任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.求证:四边形DGFE是平行四边形.
考点:三角形中位线定理,平行四边形的判定
专题:证明题
分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC且DE=
BC,GF∥BC且GF=
BC,从而得到DE∥GF,DE=GF,再利用一组对边平行且相等的四边形是平行四边形证明即可
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵D、E分别是AB、AC边的中点,
∴DE∥BC,且DE=
BC,
同理,GF∥BC,且GF=
BC,
∴DE∥GF且DE=GF,
四边形DGFE是平行四边形.
∴DE∥BC,且DE=
| 1 |
| 2 |
同理,GF∥BC,且GF=
| 1 |
| 2 |
∴DE∥GF且DE=GF,
四边形DGFE是平行四边形.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,菱形的判定以及平行四边形与菱形的关系,熟记的定理和性质是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
某种服装因换季准备打折出售,如果按原售价的七五折出售,将亏损25元,而按原售价的九折出售,将盈利20元,则该服装的成本为( )
| A、250元 | B、270元 |
| C、280元 | D、300元 |
下列四个实数中,无理数是( )
| A、-3.14 | |||
B、
| |||
C、
| |||
D、
|
 如图,数轴上的两点A、B分别表示a和b,那么A、B两点间的距离是( )
如图,数轴上的两点A、B分别表示a和b,那么A、B两点间的距离是( )| A、a+b | B、a-b |
| C、b-a | D、-b-a |

 如图,△ABC中,AB=AC,AD⊥BC于D,AE=EC,AD=18,BE=15,则△ABC的面积是
如图,△ABC中,AB=AC,AD⊥BC于D,AE=EC,AD=18,BE=15,则△ABC的面积是 解决一下问题:
解决一下问题: