Question

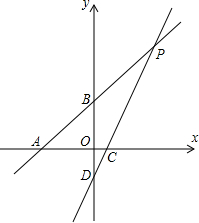如图，直线AB的函数解析式为y=x+2分别与x、y轴交于点A，点B，直线CD的函数解析为y=2x-1分别与x轴、y轴交于点C、点D，直线AB与CD相交于点P．
（1）求P点坐标；
（2）点M为x轴上一动点，当点M在什么位置时，△APM与△BDP的面积相等；
（3）若点N为线段CP上一动点，探究是否存在点N，使△ABN与△BDN的面相等？若存在，请求出点N坐标；若不存在，请说明理由．

Answer 1

分析：（1）解两个解析式组成的方程组即可求得函数的交点坐标；
（2）根据△BPD的面积即可求得AM的长，则M的坐标即可求得；
（3）设点N的坐标为（n，2n-1），则△BDN的面积可以利用n表示，然后利用n表示出△ABN的面积，根据两个三角形的面积相等，可以求得n的值，则N的坐标可以求得．

解答：解：（1）由题意可得

y=x+2 y=2x-1

，
解得

x=3 y=5

∴P点坐标是（3，5）
（2）由题意可知，点A（-2，0），B（0，2），D（0，-1），
∴BD=3，∴S△BPD=

1

2

×3×3=

9

2

，
∴

1

2

×5•AM=

9

2

，
解得AM=

9

5

，
∴点M的坐标是(-

1

5

，0)或(-

19

5

，0)
（3）存在，设点N的坐标为（n，2n-1），则S△BDN=

1

2

×3×n=

3

2

n，
而S_△ABN=S_△AOB+S_△BON-S_△AON=2+n-（2n-1）=3-n
∴

3

2

n=3-n，
解得n=

6

5

，
∴存在点N(

6

5

，

7

5

)使△ABN和△BDN面积相等．

点评：本题考查了函数图象交点的求法以及三角形的面积的计算，利用数形结合考虑问题是关键．