题目内容
直线l:m(2x-y-5)+(3x-8y-14)=0被以A(1,0)为圆心,2为半径的⊙A所截得的最短弦的长为
- A.

- B.

- C.2

- D.2

C
分析:不论m取什么值,直线l一定经过定点,首先求得这个点的坐标,判断与圆的位置关系,然后利用垂径定理即可求解.
解答:解方程组 ,解得:
,解得: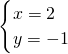 ,
,
则直线l一定经过点B(2,-1).
AB= <2,
<2,
∴B一定在⊙A的内部,当直线l与AB垂直时,直线l截得⊙A所得的弦最短,
∴最短的弦长是:2 =2
=2 .
.
故选C.
点评:本题考查了直线与垂径定理的综合应用,求得直线经过的定点B的坐标是关键.
分析:不论m取什么值,直线l一定经过定点,首先求得这个点的坐标,判断与圆的位置关系,然后利用垂径定理即可求解.
解答:解方程组
 ,解得:
,解得: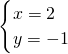 ,
,则直线l一定经过点B(2,-1).
AB=
 <2,
<2,∴B一定在⊙A的内部,当直线l与AB垂直时,直线l截得⊙A所得的弦最短,
∴最短的弦长是:2
 =2
=2 .
.故选C.
点评:本题考查了直线与垂径定理的综合应用,求得直线经过的定点B的坐标是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
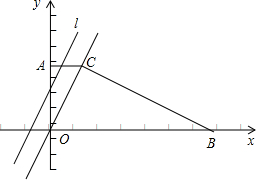 C的直线l为:y=2x+t,l由A点平移到B点时,l与直角梯形AOBC两边所围成的三角形的面积记为S.
C的直线l为:y=2x+t,l由A点平移到B点时,l与直角梯形AOBC两边所围成的三角形的面积记为S.