题目内容
直线y=
x+2,交x轴于A,交y轴于B,将直线AB绕点P(-1,0)顺时针方向旋转90°,则旋转后的直线解析式为
| 1 | 2 |
y=-2x+1
y=-2x+1
.分析:先确定A点坐标为(-4,0),再确定OA绕点P(-1,0)顺时针方向旋转90°得到对应点A′的坐标为(-1,3),由于两直线垂直时它们的一次项系数互为负倒数,得到旋转后的直线解析式y=-2x+b,然后把A′(-1,3)代入求出b即可.
解答:解:如图, A点坐标为(-4,0),则PA=3,
A点坐标为(-4,0),则PA=3,
当OA绕点P(-1,0)顺时针方向旋转90°得到对应点A′的坐标为(-1,3),
设旋转后的直线解析式y=kx+b,
则k•
=-1,
解得k=-2,
故y=-2x+b,
把A′(-1,3)代入得3=2+b,解得b=1,
故旋转后的直线解析式y=-2x+1.
故答案为y=-2x+1.
 A点坐标为(-4,0),则PA=3,
A点坐标为(-4,0),则PA=3,当OA绕点P(-1,0)顺时针方向旋转90°得到对应点A′的坐标为(-1,3),
设旋转后的直线解析式y=kx+b,
则k•
| 1 |
| 2 |
解得k=-2,
故y=-2x+b,
把A′(-1,3)代入得3=2+b,解得b=1,
故旋转后的直线解析式y=-2x+1.
故答案为y=-2x+1.
点评:本题考查了一次函数图象与几何变换:一次函数y=kx+b(k、b为常数,k≠0)的图象为直线,当直线平移时k不变,当向上平移m个单位,则平移后直线的解析式为y=kx+b+m.

练习册系列答案
相关题目
 如图,直线y=
如图,直线y=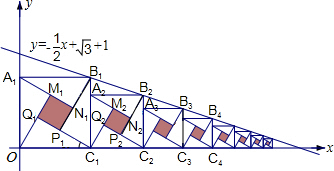 2002年在北京召开的世界数学大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线
2002年在北京召开的世界数学大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线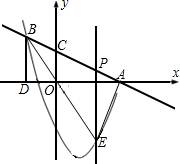 的交点是B,BD⊥x轴,垂足为D,且△ABD的面积是9.
的交点是B,BD⊥x轴,垂足为D,且△ABD的面积是9.