ЬтФПФкШн
ЁОЬтФПЁПвбжЊЙигк![]() ЕФЖўДЮКЏЪ§
ЕФЖўДЮКЏЪ§![]() (
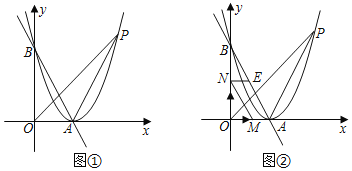
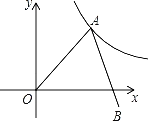
(![]() ЃО0)ЕФЭМЯѓОЙ§ЕуC(0ЃЌ1)ЃЌЧвгы
ЃО0)ЕФЭМЯѓОЙ§ЕуC(0ЃЌ1)ЃЌЧвгы![]() жсНЛгкВЛЭЌЕФСНЕуAЁЂBЃЌЕуAЕФзјБъЪЧ(1ЃЌ0)ЃЎ
жсНЛгкВЛЭЌЕФСНЕуAЁЂBЃЌЕуAЕФзјБъЪЧ(1ЃЌ0)ЃЎ
ЃЈ1ЃЉЧѓcЕФжЕКЭ![]() ЃЌ
ЃЌ![]() жЎМфЕФЙиЯЕЪНЃЛ
жЎМфЕФЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
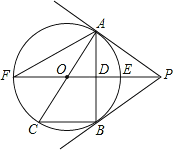
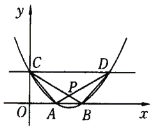
ЃЈ3ЃЉИУЖўДЮКЏЪ§ЕФЭМЯѓгыжБЯп![]() НЛгкCЁЂDСНЕуЃЌЩш AЁЂBЁЂCЁЂDЫФЕуЙЙГЩЕФЫФБпаЮЕФЖдНЧЯпЯрНЛгкЕуPЃЌМЧЁїPCDЕФУцЛ§ЮЊS1ЃЌЁїPABЕФУцЛ§ЮЊS2ЃЌЕБ0ЃМ
НЛгкCЁЂDСНЕуЃЌЩш AЁЂBЁЂCЁЂDЫФЕуЙЙГЩЕФЫФБпаЮЕФЖдНЧЯпЯрНЛгкЕуPЃЌМЧЁїPCDЕФУцЛ§ЮЊS1ЃЌЁїPABЕФУцЛ§ЮЊS2ЃЌЕБ0ЃМ![]() ЃМlЪБЃЌЧѓжЄЃКS1ЃS2ЮЊГЃЪ§ЃЌВЂЧѓГіИУГЃЪ§ЃЎ
ЃМlЪБЃЌЧѓжЄЃКS1ЃS2ЮЊГЃЪ§ЃЌВЂЧѓГіИУГЃЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃО0ЃЌЧв
ЃО0ЃЌЧв![]() Ёй1ЃЛЃЈ3ЃЉжЄУїМћНтЮіЃЌетИіГЃЪ§ЮЊ1
Ёй1ЃЛЃЈ3ЃЉжЄУїМћНтЮіЃЌетИіГЃЪ§ЮЊ1
ЁОНтЮіЁП
ЃЈ1ЃЉЗжБ№НЋAЕуКЭCЕуЕФзјБъДњШы![]() МДПЩЕУНтЃЛ
МДПЩЕУНтЃЛ
ЃЈ2ЃЉИљОнЖўДЮКЏЪ§ЕФЖЈвхМАХаБ№ЪННјааЧѓНтМДПЩЕУЕНaЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉИљОнЬтвтЃЌЗжБ№ЧѓГі![]() ЕФУцЛ§S1МА
ЕФУцЛ§S1МА![]() ЕФУцЛ§ЮЊS2ЃЌДгЖјНјааЛЏМђМДПЩЕУНт.
ЕФУцЛ§ЮЊS2ЃЌДгЖјНјааЛЏМђМДПЩЕУНт.
ЃЈ1ЃЉНЋЕу![]() ДњШы
ДњШы![]() ЕУ
ЕУ![]()
Ёр![]()
НЋЕу![]() ДњШыЕУ
ДњШыЕУ![]()
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпЖўДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгкВЛЭЌЕФСНЕу
жсНЛгкВЛЭЌЕФСНЕу
ЁрвЛдЊЖўДЮЗНГЬ![]() ЕФХаБ№ЪН
ЕФХаБ№ЪН![]()
Жј![]()
Ёр![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃО0ЃЌЧв
ЃО0ЃЌЧв![]() Ёй1ЃЛ
Ёй1ЃЛ
ЃЈ3ЃЉжЄУїЃКЁп0ЃМ![]() ЃМ1
ЃМ1
ЁрЖдГЦжсЮЊ![]() ЃО1
ЃО1
Ёр![]()
Аб![]() ДњШы
ДњШы![]() ЕУ
ЕУ![]()
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЌЁр
ЃЌЁр![]()
Ёр![]()
![]()
Ёр![]() ЮЊГЃЪ§ЃЌетИіГЃЪ§ЮЊ1.
ЮЊГЃЪ§ЃЌетИіГЃЪ§ЮЊ1.