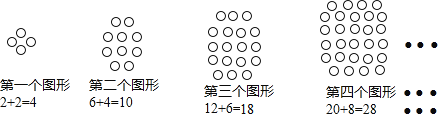
题目内容
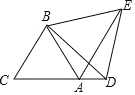
【题目】如图 ,已知△ ABC 中,点 D 、E 是 BC 边上两点,且 ADAE ,BAECAD 90 ,
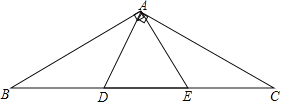
(1)试说明△ABE 与△ACD 全等的理由;
(2)如果 ADBD ,试判断△ADE 的形状,并说明理由.
【答案】(1)见解析;(2)△ ADE 是等边三角形.理由见解析.
【解析】
(1)由ADAE得到AED ADE,再由BAECAD 90 即可得到△ABE ≌△ACD;
(2) 由AD BD 得到BAD B,依据三角形内角和求得AED 60 可得到△ADE是等边三角形.
(1)∵ AD AE (已知),
∴AED ADE (等边对等角).
在△ABE 和△ACD 中
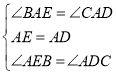 ,
,
∴△ABE ≌△ACD(ASA);
(2)△ADE是等边三角形.
理由:∵AD BD ,
∴BAD B(等边对等角).
设B 的度数为 x ,则BAD 的度数为 x .
∵ADE B BAD( 三角形的一个外角等于与它不相邻的两个内角的和),
∴ADE AED 2x .
∵B AEB BAE 180(三角形的内角和等于 180°),
∴ x 2x 90 180,
解得 x 30 ,
∴AED 60 .
∵AD AE(已知),
∴△ADE 是等边三角形(有一个内角等于 60°的等腰三角形是等边三角形).

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?