题目内容
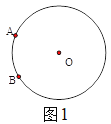
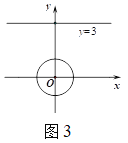
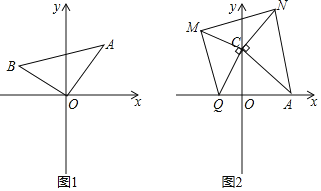
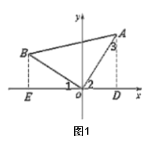
【题目】(1)如图1,等腰直角三角形![]() 的直角顶点
的直角顶点![]() 在坐标原点,点
在坐标原点,点![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标.
的坐标.
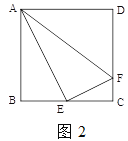
(2)依据(1)的解题经验,请解决下面问题:
如图2,点![]() ,
,![]() 两点均在
两点均在![]() 轴上,且
轴上,且![]() ,分别以
,分别以![]() 为腰在第一、第二象限作等腰
为腰在第一、第二象限作等腰![]() ,
,![]() 连接
连接![]() ,与
,与![]() 轴交于点
轴交于点![]() 的长度是否发生改变?若不变,求
的长度是否发生改变?若不变,求![]() 的值;若变化,求
的值;若变化,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)9
;(2)9
【解析】
(1)过B作BE⊥x轴于E,过A作AD⊥x轴于D.只要证明Rt△BEO≌Rt△ADO即可解决问题;
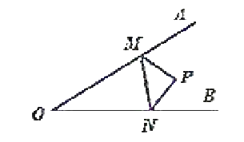
(2)过M作MD⊥y轴于D,过N作NB⊥y轴于B.只要证明△BNP≌△DMP即可解决问题;
(1)如图1,过![]() 作
作![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]()
∴![]()
又∵等腰直角![]()
∴![]() ,
,![]()
又∵![]()
∴![]()
在![]() 与
与![]() 中
中
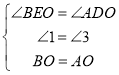
∴![]() ≌
≌![]()
∴![]()
![]()
又∵![]()
∴![]() ,
,![]()
又∵![]() 在第二象限
在第二象限
∴![]()
(2)如图2,过![]() 作
作![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]()
由(1)知:![]() ,
,![]() ,
,![]()
∴![]() 与
与![]() 中
中
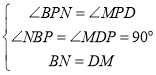
∴![]() ≌
≌![]()
∴![]()
![]()
∴![]()
而![]() ①
①
![]() ②
②
∴![]() ,
, ![]()
∴![]()
即:![]() 的值不变总等于9.
的值不变总等于9.


练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目