题目内容
15.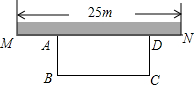 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,①试设计一种砌法,使矩形花园的面积为300m2.
②请设计一种砌法,使矩形花园的面积最大.
分析 (1)根据题意可以得到相应的一元二次方程,从而可以解答本题;
(2)根据题意可以得到面积与矩形一边长的关系式,然后化为顶点式,注意求出的边长要符合题意.
解答 解:(1)设AB为xm,则BC为(50-2x)m,
x(50-2x)=300,
解得,x1=10,x2=15,
当x1=10时50-2x=30>25(不合题意,舍去),
当x2=15时50-2x=20<25(符合题意),
答:当砌墙宽为15米,长为20米时,花园面积为300平方米;
(2)设AB为xm,矩形花园的面积为ym2
则y=x(50-2x)=-2(x-$\frac{25}{2}$)2+$\frac{625}{2}$,
∴x=$\frac{25}{2}$时,此时y取得最大值,50-2x=25符合题意,此时y=$\frac{625}{2}$,
即当砌墙的宽为$\frac{25}{2}$米,长为25米时,矩形花园的面积最大.
点评 本题考查二次函数的应用、一元二次方程的应用,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
5.如图,边长为x+2的正方形纸片剪出一个边长为x的正方形后,剩余部分可剪拼成一个长方形,则拼成的长方形的面积为( )
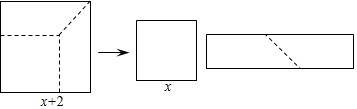

| A. | 2x+2 | B. | 4x+4 | C. | x+4 | D. | 2x-2 |
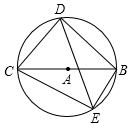 如图,四边形BDCE内接于以BC为直径的⊙A,已知:BC=10,cos∠BCD=$\frac{3}{5}$,∠BCE=30°,则线段DE的长是3+4$\sqrt{3}$.
如图,四边形BDCE内接于以BC为直径的⊙A,已知:BC=10,cos∠BCD=$\frac{3}{5}$,∠BCE=30°,则线段DE的长是3+4$\sqrt{3}$.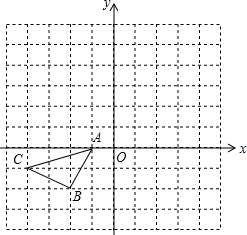 在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题.
在如图所示的正方形格中,△ABC的顶点均在格点上请在所给直角坐标系中按要求画图和解答下列问题.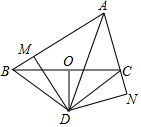 如图,△ABC中,点O在边BC上,OD垂直平分BC,AD平分∠BAC,过点D分别作DM⊥AB于点M,DN⊥AC于点N.
如图,△ABC中,点O在边BC上,OD垂直平分BC,AD平分∠BAC,过点D分别作DM⊥AB于点M,DN⊥AC于点N.