��Ŀ����
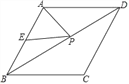
��ͼ����֪����ABCD���ܳ�Ϊ16�����Ϊ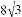 ��EΪAB���е㣬��PΪ�Խ���BD��һ���㣬��EP+AP����СֵΪ��������
��EΪAB���е㣬��PΪ�Խ���BD��һ���㣬��EP+AP����СֵΪ��������
A. 2 B. 2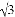 C. 4 D. 4
C. 4 D. 4
���𰸡�B
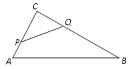
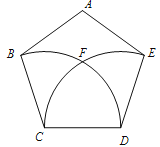
�������������������ͼ��CE���AB��E�䣬��BD��P�䣬����AC��AP�䣮
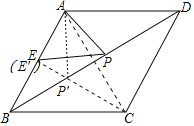
����֪����ABCD���ܳ�Ϊ16�����Ϊ8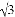 ��
��
��AB=BC=4��AB•CE��=8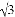 ��
��
��CE��=2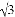 ��
��
��Rt��BCE����BE��=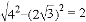 ��
��
��BE=EA=2��
��E��E���غϣ�
���ı���ABCD�����Σ�
��BD��ֱƽ��AC��
��A��C����BD�Գƣ�
�൱P��P���غ�ʱ��P��A+P��E��ֵ��С����СֵΪCE�ij�=2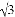 ��
��
��ѡ��B��
�����͡���ѡ��
��������
11
9��ƽ������_____��
��ϰ��ϵ�д�
�����Ŀ



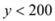 ʱ����
ʱ����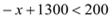 ��
�� 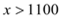
 ��
��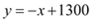 ����
����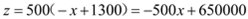
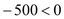 ���൱
���൱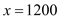 ʱ��z��ͣ���
ʱ��z��ͣ���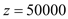 ��
��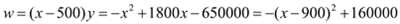
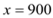 ʱ��
ʱ��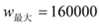 .
. 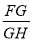 ��ֵ��
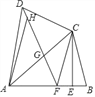
��ֵ��
 )��2��
)��2��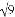 +��
+��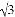 ��4��0��
��4��0��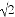 cos45�㣮
cos45�㣮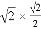
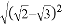 =�� ��
=�� ��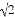 ��
�� 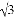 D.
D. 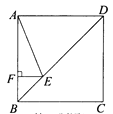
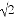 C. 4��2
C. 4��2