题目内容
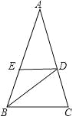
【题目】如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB
(1)求证:DE与⊙O相切;
(2)若∠C=30°,求∠BOD的度数;
(3)在(2)的条件下,若⊙O半径为2,求阴影部分面积.
【答案】
(1)证明:连结OD,

∵AB为⊙O为直径,
∴∠ADB=∠BDC=90°,
又∵E是斜边BC的中点
∴DE=BE=CE,
∴∠BDE=∠DBE,
∵OD=OB,
∴∠ODB=∠OBD
∴∠ODE=∠ODB+∠BDE=∠OBD+∠DBE=∠ABC=90°
即DE与⊙O相切.
(也可以通过证明△OBE≌△ODE得到∠ODE=∠OBE=90°)
(2)解:若∠C=30°而DE=CE,
∴∠DEB=60°
在四边形OBED中,则∠BOD=360°﹣90°﹣90°﹣60°=120°
(3)解:连结OE,则∠OED=∠OEB=30°
∵OD=OB=2∴DE=BE=2 ![]()
∴S阴影部分=S四边形OBED﹣S扇形OBD=S△OBE+S△ODE﹣S扇形OBD
=2 ![]() +2
+2 ![]() ﹣
﹣ ![]() =4
=4 ![]() ﹣
﹣ ![]() .
.
【解析】(1)要证明DE与与⊙O相切;只要证明∠ODE=∠ODB+∠BDE=∠OBD+∠DBE=∠ABC=90°即可;(2)在四边形OBED中,利用四边形的内角和求∠BOD即可;(3)用S阴影部分=S四边形OBED﹣S扇形OBD=S△OBE+S△ODE﹣S扇形OBD计算即可。
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线,以及对扇形面积计算公式的理解,了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】郴州市一座美丽的旅游城市,吸引了很多的外地游客,某旅行社对5月份本社接待的外地游客来郴州旅游的首选景点作了一次抽样调查.调查结果如下图表:(如图)
景点 | 频数 | 频率 |
东江湖 |
|
|
莽山 |
|
|
飞天山 |
| |
苏仙岭 |
|
|
万华岩 |
|
|

![]() 此次共调查了多少人?
此次共调查了多少人?
![]() 请将以上图表补充完整.
请将以上图表补充完整.
![]() 该旅行社预计6月份接待外地来郴的游客
该旅行社预计6月份接待外地来郴的游客![]() 人,请你估计首选去东江湖的人数约有多少人.
人,请你估计首选去东江湖的人数约有多少人.