Question

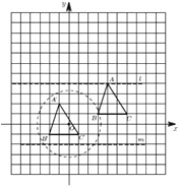
【题目】正方形网格中，每个小正方形的边长为1个单位长度建立如图所示的平面直角坐标系，的顶点均为格点，把向左平移5个单位长度，再向下平移2个单位长度，得到．

（1）在图中画出；

（2）点在轴上，且与的面积相等，则点的坐标为 ；

（3）横、纵坐标均为整数的点称为整数点，在第一象限中的整数点满足，直接写出整数点的所有可能坐标．

Answer 1

【答案】（1）画图见解析

（2）；

（3），，，

【解析】

（1）把每个顶点向左平移5个单位长度，再向下平移2个单位长度，连接平移后的三个顶点，即可得到．

（2）与的面积相等，且它们由公共的底边，点P到BC边的距离为3，且点在轴上，即可求得点P的坐标．

（3）采用作图的方式，点在以为圆心、为直径的圆内，又点在第一象限，即可确定M符合条件的点．

（1）如图所示，即为所求：

（2）与的面积相等，且它们由公共的底边，

∴两三角形在边上的高相等

即点P到BC边的距离为3，

又∵点在轴上，

可得点P的坐标为或，

故答案为：或．

（3）如图，点在以为圆心、为直径的圆内，又点在第一象限，所以点的坐标为，，，．

故答案为：，，，