题目内容
已知:抛物线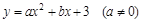 与
与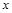 轴交于A(1,0)和B(
轴交于A(1,0)和B(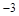 ,0)点,与
,0)点,与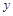 轴交于C点
轴交于C点
(1)求出抛物线的解析式;
(2)设抛物线对称轴与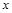 轴交于M点,在对称轴上是否存在P点,使
轴交于M点,在对称轴上是否存在P点,使 为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
(3)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求此时点E 的坐标.
【答案】
解:(1)抛物线的解析式为 .(2分)
.(2分)
(2)存在.
符合条件的点 为(-1,
为(-1, )或
)或 或
或 或(-1,6).(各1分)
或(-1,6).(各1分)
(3)过点E作EF
 轴于点F,设E(
轴于点F,设E( ,y)(-3<x<0)
,y)(-3<x<0)
则

 时,
时,
把 代入
代入 中,
中,
 点的坐标为
点的坐标为 (2分)
(2分)
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
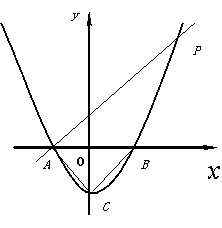 (3)在线段AP上是否存在一点M,使,△MBC的周长最小,若存在,请求出点M的坐标;若不存在,请说明理由.
(3)在线段AP上是否存在一点M,使,△MBC的周长最小,若存在,请求出点M的坐标;若不存在,请说明理由.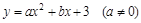 与
与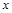 轴交于A(1,0)和B(
轴交于A(1,0)和B(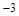 ,0)点,与
,0)点,与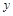 轴交于C点
轴交于C点 为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;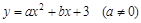 与
与 轴交于A(1,0)和B(
轴交于A(1,0)和B( ,0)点,与
,0)点,与 轴交于C点
轴交于C点 为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;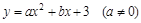 与
与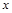 轴交于A(1,0)和B(
轴交于A(1,0)和B( ,0)点,与
,0)点,与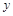 轴交于C点
轴交于C点 为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;