题目内容
已知,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于C点.
轴交于C点.
(1)求点A、B、C三点的坐标;
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积;
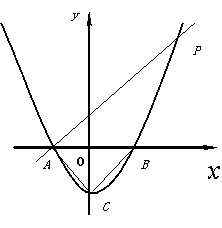 (3)在线段AP上是否存在一点M,使,△MBC的周长最小,若存在,请求出点M的坐标;若不存在,请说明理由.
(3)在线段AP上是否存在一点M,使,△MBC的周长最小,若存在,请求出点M的坐标;若不存在,请说明理由.
解:(1)当y=0时,x2-1=0,解得x1=1,x2=﹣1.
∴A点坐标为(-1,0),B点坐标为(1,0).
当x=0时,y=02-1=﹣1,
∴C点坐标为(0,﹣1).
(2)过点P作PQ⊥![]() 轴于点Q.
轴于点Q.
∵AO=BO=CO=1,∠AOC=∠BOC=90°,
∴∠OAC=∠OCA=∠OCB=45°,
∴∠ACB=∠OCA+∠OCB=90°,
∵AP∥CB,
∴∠PAC=180°﹣∠ACB=90°![]() ,
,
∴四边形ACBP是直角梯形.
∴∠PAQ=∠PAC-∠CAB=45°.
∵∠AQP=90°,
∴PQ=AQ.
设P点(a,a2-1),则AQ=OA+OQ=1+ a.
∵AQ=PQ,
∴1+ a= a2-1,解得a1=2,a2=-1;
∵点P在第一象限,∴a=2.
∴P点坐标为(2,3),∴AP=3![]() .
.
∵AC=BC=![]() ,S四边形ACBP=4.
,S四边形ACBP=4.
(3)存在.延长CA到点C’,使AC’=AC,过点C’作C’D⊥![]() 轴于点D,连接
轴于点D,连接![]() BC’,则BC’与AP的交点即为M点.
BC’,则BC’与AP的交点即为M点.
∵∠PAC=90°,
∴C与C’关于AP对称.
∵∠C’AD=∠CAO, ∠C’DA=∠COA,C’A=CA,
∴△C‘DA≌△COA.
∴DA=OA=1,C’D=CO=1,∴OD=OA+AD=2,
∴C’点坐标为(﹣2,1) .
∴直线AP与直线BC’的解析式分别为![]() ;
;![]() .
.
∴解方程组可得点M的坐标为(![]() ,
,![]() ).
).
∴在线段AP上存在一点M(![]() ,
,![]() ),使△MBC的周长最小.
),使△MBC的周长最小.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案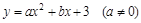 与
与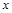 轴交于A(1,0)和B(
轴交于A(1,0)和B(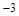 ,0)点,与
,0)点,与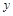 轴交于C点
轴交于C点 为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;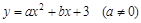 与
与 轴交于A(1,0)和B(
轴交于A(1,0)和B( ,0)点,与
,0)点,与 轴交于C点
轴交于C点 为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;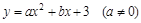 与
与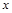 轴交于A(1,0)和B(
轴交于A(1,0)和B( ,0)点,与
,0)点,与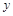 轴交于C点
轴交于C点 为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;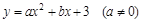 与
与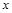 轴交于A(1,0)和B(
轴交于A(1,0)和B(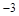 ,0)点,与
,0)点,与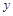 轴交于C点
轴交于C点 为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;