题目内容
4. 如图,⊙O的直径AB=10,CD是⊙O的弦,CD⊥AB,垂足为P,且OP=4,则CD的长为( )
如图,⊙O的直径AB=10,CD是⊙O的弦,CD⊥AB,垂足为P,且OP=4,则CD的长为( )| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
分析 连接OC,由垂径定理得出PC=PD=$\frac{1}{2}$CD,由勾股定理求出PC,即可得出CD的长.
解答 解:连接OC,如图所示:
∵CD⊥AB,
∴PC=PD=$\frac{1}{2}$CD,∠OPC=90°,
∵⊙O的直径AB=10,
∴OC=5,
由勾股定理得:PC=$\sqrt{O{C}^{2}-O{P}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴CD=2PC=6.
故选:C.
点评 本题考查了垂径定理、勾股定理;熟练掌握垂径定理,由勾股定理求出PC是解决问题的关键.

练习册系列答案
相关题目
12.比a的$\frac{1}{2}$大5的数是( )
| A. | $\frac{1}{2}$a+5 | B. | a$({\frac{1}{2}+5})$ | C. | $({a+\frac{1}{2}})$+5 | D. | $\frac{1}{2}$(a+5) |
14.已知a-b=7,c-d=-3,则(a+c)-(b+d)的值是( )
| A. | 4 | B. | -4 | C. | -10 | D. | 10 |
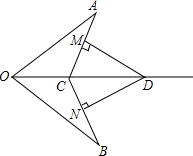 如图,已知C,D在∠AOB的平分线上,OA=OB,DM⊥AC于点M,DN⊥BC于点N.求证:DM=DN.
如图,已知C,D在∠AOB的平分线上,OA=OB,DM⊥AC于点M,DN⊥BC于点N.求证:DM=DN.