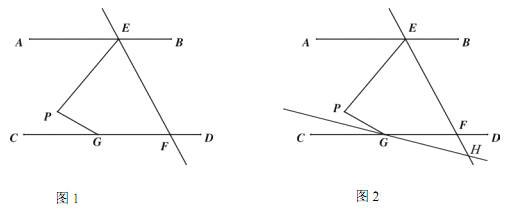题目内容
【题目】如图1,在![]() 中,
中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,则
,则![]() 的度数为______;
的度数为______;
(2)若![]() ,直线
,直线![]() 经过点
经过点![]() .
.
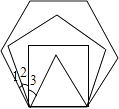
①如图2,若![]() ,求
,求![]() 的度数(用含
的度数(用含![]() 的代数式表示);
的代数式表示);
②如图3,若![]() 绕点
绕点![]() 旋转,分别交线段
旋转,分别交线段![]() 于点
于点![]() ,试问在旋转过程中
,试问在旋转过程中![]() 的度数是否会发生改变?若不变,求出
的度数是否会发生改变?若不变,求出![]() 的度数(用含
的度数(用含![]() 的代数式表示),若改变,请说明理由:
的代数式表示),若改变,请说明理由:
③如图4,继续旋转直线![]() ,与线段
,与线段![]() 交于点
交于点![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 的关系(用含
的关系(用含![]() 的代数式表示).
的代数式表示).

【答案】(1)130°;(2)①90![]() -
-![]() ;②不变,90
;②不变,90![]() -
-![]() ;③∠NDC+∠MDB=90
;③∠NDC+∠MDB=90![]() -
-![]() .
.
【解析】
(1)根据已知,以及三角形内角和等于180![]() ,即可求解;
,即可求解;
(2)①根据平行线的性质可以证得∠ABD=∠BDM=∠MBD,∠CND=∠A=![]() ,再利用含有
,再利用含有![]() 的式子分别表示出∠NDC、∠MDB,进行作差,即可求解代数式;
的式子分别表示出∠NDC、∠MDB,进行作差,即可求解代数式;
②延长BD交AC于点E,则∠NDE=∠MDB,因此∠NDC-∠MDB=∠NDC-∠NDE=∠EDC,再利用三角形内角和为180![]() ,即可求解;
,即可求解;
③如图可知,∠NDC+∠MDB=180![]() -∠BDC,利用平角的定义,即可求解代数式.
-∠BDC,利用平角的定义,即可求解代数式.
解:(1)∵∠A=80![]()
∴∠ABC+∠ACB=180![]() -80
-80![]() =100
=100![]()
又∵ BD平分∠ABC,CD平分∠ACB,
∴∠DBC+∠DCB=![]() 100
100![]() =50
=50![]() .
.
∴ ∠BDC=180![]() -50
-50![]() =130
=130![]() .
.
(2)①∵MN//AB,BD平分∠ABC,CD平分∠ACB,
∴∠ABD=∠BDM=∠MBD,∠CND=∠A=![]() ,
,
∴ ∠NDC=180![]() -
-![]() -
-![]() ∠ACB,∠MDB=
∠ACB,∠MDB=![]() ∠ABC,
∠ABC,
∴∠NDC-∠MDB=180![]() -
-![]() -
-![]() ∠ACB-
∠ACB-![]() ∠ABC=180
∠ABC=180![]() -
-![]() -
-![]() (∠ACB+∠ABC)=180
(∠ACB+∠ABC)=180![]() -
-![]() -
-![]() (180
(180![]() -
-![]() )=90
)=90![]() -
-![]() .
.
②不变;延长BD交AC于点E,如图:

∴∠NDE=∠MDB,
∵∠BDC=180![]() -
-![]() (∠ACB+∠ABC)=180
(∠ACB+∠ABC)=180![]() -
-![]() (180
(180![]() -
-![]() )=90
)=90![]() +
+![]() ,
,
∴∠NDC-∠MDB=∠NDC-∠NDE=∠EDC=180![]() -∠BDC=180
-∠BDC=180![]() -(90
-(90![]() +
+![]() )=90
)=90![]() -
-![]() ,
,
同①,说明MN在旋转过程中∠NDC-∠MDB的度数只与∠A有关系,而∠A始终不变,
故:MN在旋转过程中∠NDC-∠MDB的度数不会发生改变.
③如图可知,∠NDC+∠MDB=180![]() -∠BDC,
-∠BDC,
由②知∠BDC=90![]() +
+![]() ,
,
∴∠NDC+∠MDB=180![]() -(90
-(90![]() +
+![]() )=90
)=90![]() -
-![]() .
.
故∠NDC与∠MDB的关系是∠NDC+∠MDB=90![]() -
-![]() .
.

 名校课堂系列答案
名校课堂系列答案