题目内容
【题目】如图，正方形ABCD的面积为4，其面积标记为S1 ， 以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2 ， …，按照此规律继续下去，则S10的值为 ．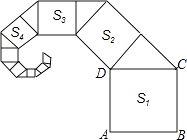 
【答案】
【解析】解：观察，发现：S1=4，则正方形ABCD的边长为2，
S2=（2× 
）2=2，S3=（ 
× ）2=1，S4=（1× ）2= 
，…，
∴Sn=[2×（ ）n﹣1]2=4×（ ）n﹣1，
∴S10=4×（ ）10﹣1= ．
故答案是： ．
【考点精析】关于本题考查的等腰直角三角形和正方形的性质，需要了解等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案．
练习册系列答案
相关题目
