题目内容
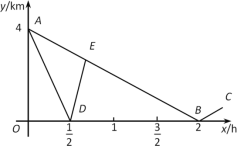
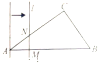
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,直线l经过点A,且垂直于AB,分别与AB、AC相交于点M,N.直线l从点A出发,沿AB方向以1cm/s的速度向点B运动,当直线l经过点B时停止运动,若运动过程中△AMN的面积是y(cm2),直线l的运动时间是x(s)则y与x之间函数关系的图象大致是( )
A.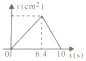 B.
B.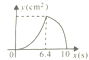
C.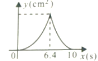 D.
D.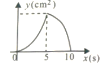
【答案】B
【解析】
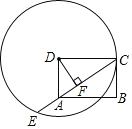
过点C作CD⊥AB于D.先证明△ABC是直角三角形,进而求出CD、AD的长.然后分![]() 和
和![]() 两种情况,求出MN的长,根据三角形面积公式即可得出y与x的函数关系式,进而得出结论.
两种情况,求出MN的长,根据三角形面积公式即可得出y与x的函数关系式,进而得出结论.
过点![]() 作
作![]() 于
于![]() .
.
∵![]() ,
,
∴![]() 是直角三角形,
是直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .分两种情况:
.分两种情况:
(1)当![]() 时,如图1.
时,如图1.
∵![]() ,
,
∴![]() ,
,
∴![]() ,函数图象是开口向上,对称轴为
,函数图象是开口向上,对称轴为![]() 轴,位于
轴,位于![]() 轴右侧的抛物线的一部分;
轴右侧的抛物线的一部分;
(2)当![]() 时,如图2.
时,如图2.
∵![]() ,
,
∴![]() ,
,
∴![]() ,函数图象是开口向下,对称轴为直线
,函数图象是开口向下,对称轴为直线![]() ,位于对称轴右侧的抛物线的一部分;综上所述:B选项符合题意.
,位于对称轴右侧的抛物线的一部分;综上所述:B选项符合题意.
故选:B.



练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目