题目内容
【题目】如图，PA、PB、CD是⊙O的切线，切点分别是A、B、E，CD分别交PA、PB于C、D两点，若∠APB=60°，则∠COD的度数（ ）
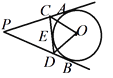
A. 50° B. 60° C. 70° D. 75°
【答案】B
【解析】
连接AO，BO，OE由切线的性质可得∠PAO=∠PBO=90°，结合已知条件和四边形的内角和为360°可求出∠AOB的度数，再由切线长定理即可求出∠COD的度数．
连接AO,BO,OE,
∵PA、PB是O的切线，
∴∠PAO=∠PBO=90°，
∵∠APB=60°，
∴∠AOB=360°2×90°60°=120°，
∵PA、PB、CD是O的切线，
∴∠ACO=∠ECO，∠DBO=∠DEO，
∴∠AOC=∠EOC，∠EOD=∠BOD，
∴∠COD=∠COE+∠EOD=
∠AOB=60°.
故选B.
练习册系列答案
春雨教育同步作文系列答案
相关题目
