题目内容
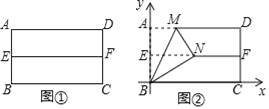
【题目】如图,在矩形![]() 中,点
中,点![]() 是边
是边![]() 上一点(不与点
上一点(不与点![]() 重合),点
重合),点![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,连接
,连接![]() .
.
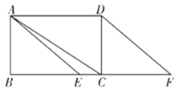
(1)求证:![]()
(2)连接![]() ,其中
,其中![]()
①当四边形![]() 是菱形时,求线段
是菱形时,求线段![]() 与线段
与线段![]() 之间的距离;
之间的距离;
②若点![]() 是
是![]() 的内心,连接
的内心,连接![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)①线段![]() 与线段
与线段![]() 之间的距离为
之间的距离为![]() ,②
,②![]() .
.
【解析】
(1)根据已知,利用SAS即可证明;
(2)①因为四边形![]() 是菱形,所以AE与DF的距离等于AD与EF之间的距离,即CD为所求,再利用勾股定理即可求解;
是菱形,所以AE与DF的距离等于AD与EF之间的距离,即CD为所求,再利用勾股定理即可求解;
②如图作出辅助线,根据△ABE![]() △DCF(SAS),
△DCF(SAS),![]() 的取值范围即可转化为在△ABE中进行求解,找到E点在B、C两点临界处的∠AED的取值范围,利用三角形内角和=180
的取值范围即可转化为在△ABE中进行求解,找到E点在B、C两点临界处的∠AED的取值范围,利用三角形内角和=180![]() ,即可求得.
,即可求得.
(1)证明:∵四边形ABCD是矩形,
∴AB=DC, ∠B=∠BCD=90![]() ,
,
∴∠B=∠DCF=90![]() ,
,
∵BE=CF,
∴△ABE![]() △DCF(SAS).
△DCF(SAS).
(2)解:①∵四边形AEFD是菱形,
∴ AE与DF的距离等于AD与EF之间的距离,即CD的长,
∵AC=![]() ,BC=AD=6,在△ADC中,
,BC=AD=6,在△ADC中,
∴![]() ,
,
∴线段AE与线段DF之间的距离为![]() .
.
②∵△ABE![]() △DCF,
△DCF,
∴△DCF的内心即为△ABE的内心,
如图:作出∠AEB、∠ABE的角平分线BQ、EQ,
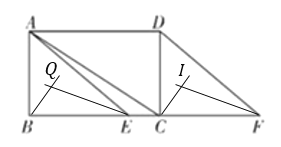
则∠BQE=∠CIF, ∠BQE即为所求,
∵∠ABE恒等于90![]() ,
,
∴![]() ∠ABE恒等于45
∠ABE恒等于45![]() ,
,
∵当点E在点B处时,∠AEB=90![]() ,
,
当点E在点C处时,在Rt△ABE 中,AB=![]() AC,知∠AEB=30
AC,知∠AEB=30![]() ,
,
∴所以30![]() ∠AEB
∠AEB![]() ,
,
∴15![]() ∠AEB
∠AEB![]() ,
,
∴ ![]() ∠ABE+
∠ABE+![]() ∠AEB
∠AEB![]() ,
,
即![]() ∠ABE+
∠ABE+![]() ∠AEB
∠AEB![]() ,
,
而∠BQE=180![]() -
-![]() ∠ABE+
∠ABE+![]() ∠AEB,
∠AEB,
∴![]() ∠BQE
∠BQE![]() ,
,
即![]() ∠BQE
∠BQE![]() .
.
即![]() ∠CIF
∠CIF![]() .
.
故 90![]() ∠CIF
∠CIF![]() .
.

练习册系列答案
相关题目