题目内容
16.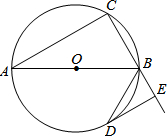 已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于点D,DE⊥CB的延长线于点E.
已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于点D,DE⊥CB的延长线于点E.(1)求证:DE为⊙O的切线;
(2)若∠A=30°,BE=3,分别求线段DE和$\widehat{BD}$的长.
分析 (1)连接OD,DC,CO,首先证明AC∥DE可得∠ECD=∠ODC,根据直角三角形两锐角互余可得∠CDE+∠DCE=90°,利用等量代换可得∠ODC+∠CDE=90°,进而可得DE为⊙O的切线;
(2)首先证明∠DBE=60°,然后利用三角函数可得BD和DE长,再利用弧长公式可得$\widehat{BD}$的长.
解答 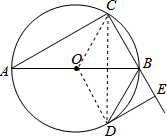 (1)证明:连接OD,DC,CO,
(1)证明:连接OD,DC,CO,
∵OC=OD,
∴∠OCD=∠ODC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥CB,
∴∠DEC=90°,
∴AC∥DE,∠CDE+∠DCE=90°,
∴∠ECD=∠ODC,
∴∠ODC+∠CDE=90°,
∴DE为⊙O的切线;
(2)解:∵∠A=30°,∠ACB=90°,
∴∠ABE=120°,
∵BD平分∠ABE,
∴∠ABD=∠DBE=60°,
∵BE=3,
∴DE=EB•tan60°=3$\sqrt{3}$,BD=6,
∵DO=BO,
∴∠BOD=60°,
∴$\widehat{BD}$=$\frac{60π×6}{180}$=2π.
点评 此题主要考查了弧长计算、切线的判定、以及三角函数的应用,关键是掌握切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
7. 如图,直线a∥b,则∠ABD的度数是( )
如图,直线a∥b,则∠ABD的度数是( )
 如图,直线a∥b,则∠ABD的度数是( )
如图,直线a∥b,则∠ABD的度数是( )| A. | 80° | B. | 100° | C. | 112° | D. | 132° |
6.下列事件是不可能事件的是( )
| A. | 买一张彩票不可能中奖 | B. | 明天会下雨 | ||
| C. | 打开电视正在播广告 | D. | 度量三角形的内角和结果是360° |
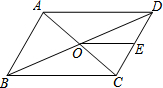 如图,已知?ABCD的对角线AC、BD相交于点O,点E是CD的中点,若BD=12cm,△DOE的周长为15cm,则?ABCD的周长为36cm.
如图,已知?ABCD的对角线AC、BD相交于点O,点E是CD的中点,若BD=12cm,△DOE的周长为15cm,则?ABCD的周长为36cm. 如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字.请认真观察此图,写出(a+b)3的展开式(a+b)3=a3+3a2b+3ab2+b3.
如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字.请认真观察此图,写出(a+b)3的展开式(a+b)3=a3+3a2b+3ab2+b3.
