题目内容
18.已知Rt△两边的长分别是6、8,则第三边的长是10或2$\sqrt{7}$.分析 分两种情况:①当6和8为两条直角边长时,由勾股定理求出斜边长即可;②当8为斜边长时,由勾股定理求出第三边的长即可.
解答 解:分两种情况:
①当6和8为两条直角边长时,
第三边长=斜边长=$\sqrt{{6}^{2}+{8}^{2}}$=10;
②当8为斜边长时,
第三边的长=$\sqrt{{8}^{2}-{6}^{2}}$=2$\sqrt{7}$;
综上所述:第三边的长为10或2$\sqrt{7}$;
故答案为:10或2$\sqrt{7}$.
点评 本题考查了勾股定理;熟练掌握勾股定理,通过分类讨论求出第三边的长是解决问题的关键.

练习册系列答案
相关题目
9.下列各组图形中,属于全等图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.下列说法正确的是( )
| A. | 8的平方根是±2 | B. | -7是49的平方根 | ||
| C. | 立方根等于它本身的数只有0和1 | D. | $\sqrt{81}$的算术平方根是9 |
10.一元二次方程x2-2x-3=0的根的情况是( )
| A. | 无实根 | B. | 有两相等实根 | C. | 有两不等实根 | D. | 无法判断 |
 如图,作出格点△ABC关于直线MN的对称图形△A′B′C′(不写作法).
如图,作出格点△ABC关于直线MN的对称图形△A′B′C′(不写作法).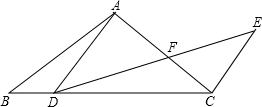 如图,在△ABC中,AB=AC=10,cosB=$\frac{4}{5}$,点D、F为边BC、AC上一点,∠ADF=∠B,BD=4.
如图,在△ABC中,AB=AC=10,cosB=$\frac{4}{5}$,点D、F为边BC、AC上一点,∠ADF=∠B,BD=4.