题目内容
如图，在图1所示的正方形铁皮上剪下一个圆形和扇形，使之恰好围成图2所示的一个圆锥模型．设圆的半径为r，扇形的半径为R，则圆的半径与扇形的半径之间的关系为（ ）
A．R=2r
B．R=
rC．R=3r
D．R=4r
【答案】分析：根据弧长公式计算．
解答：解：因为扇形的弧长等于圆锥底面周长，
所以
×2πR=2πr，
化简得R=4r．
故选D．
点评：圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把的扇形的弧长等于圆锥底面周长作为相等关系，列方程求解．
解答：解：因为扇形的弧长等于圆锥底面周长，
所以
×2πR=2πr，化简得R=4r．
故选D．
点评：圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把的扇形的弧长等于圆锥底面周长作为相等关系，列方程求解．
练习册系列答案
相关题目
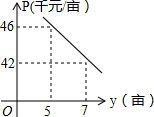为响应薄熙来书记建设“森林重庆”的号召，某园艺公司从2010年9月开始积极进行植树造林．该公司第x月种植树木的亩数y（亩）与x之间满足y=x+4，（其中x从9月算起，即9月时x=1，10月时x=2，…，且1≤x≤6，x为正整数）．由于植树规模扩大，每亩的收益P（千元）与种植树木亩数y（亩）之间存在如图（25题图）所示的变化趋势．
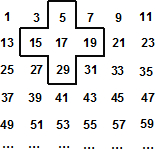将连续的奇数1，3，5，7，…，排成如下图的数表，用图中所示的十字框可任意框出5个数．
x +c的图象F交x轴于B、C两点，交y轴于M点，其中B（-3，0），M（0，-1）。已知AM=BC。
的值；
x
+c的图象F交x轴于B、C两点，交y轴于M点，其中B（-3，0），M（0，-1）。已知AM=BC。
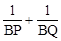的值；
