题目内容
20.已知一次函数y=kx+b的图象经过点A(-2,4)和直线y=-3x+1与y轴的交点.(1)求一次函数y=kx+b的解析式;
(2)判断点P(2a,4a-4)是否在这个一次函数的图象上,并说明理由.
分析 (1)先求出直线y=-3x+1与y轴的交点坐标,再把(-2,4)、(0,1)分别代入y=kx+b得到关于k和b的方程组,然后解方程组求出k、b即可得到一次函数解析式;
(2)先计算出当x=2a时,y=-3a+1,根据一次函数图象上点的坐标特征,当-3a+1=4a-4时,点P(2a,4a-4)在这个一次函数的图象上,解方程可求出此时a的值,反之不在.
解答 解:(1)当x=0时,y=-3x+1=1,则直线y=-3x+1与y轴的交点坐标为(0,1),
把(-2,4)、(0,1)分别代入y=kx+b得$\left\{\begin{array}{l}{-2k+b=4}\\{b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=1}\end{array}\right.$,
所以所求一次函数的解析式为y=-$\frac{3}{2}$x+1;
(2)当x=2a时,y=-$\frac{3}{2}$x+1=-$\frac{3}{2}$×2a+1=-3a+1,若-3a+1=4a-4,解得a=$\frac{5}{7}$,
所以当a=$\frac{5}{7}$时,点P(2a,4a-4)在这个一次函数的图象上;当a≠$\frac{5}{7}$时,点P(2a,4a-4)不在这个一次函数的图象上.
点评 本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.
也考查了一次函数图象上点的坐标特征.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
10.0.5的倒数为( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
11.不等式组$\left\{\begin{array}{l}{-2x<6}\\{2-x<0}\end{array}\right.$的解集是( )
| A. | x<-3 | B. | x>-3 | C. | x<2 | D. | x>2 |
5.若一次函数y=2mx+(m2-2m)的图象经过坐标原点,则( )
| A. | m=0或m=2 | B. | m=0 | C. | m=2 | D. | 无法确定 |
10.一根头发丝的直径约为0.00 006纳米,用科学记数法表示0.00 006,正确的是( )
| A. | 6×10-6 | B. | 6×10-5 | C. | 6×10-4 | D. | 0.6×10-4 |
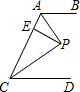 如图,AB∥CD,AP、CP分别是∠BAC和∠ACD的平分线,PE⊥AC于E,且PE=5cm,则AB与CD之间的距离是10cm.
如图,AB∥CD,AP、CP分别是∠BAC和∠ACD的平分线,PE⊥AC于E,且PE=5cm,则AB与CD之间的距离是10cm.