题目内容
13.解下列方程(1)x2-5x-6=0
(2)(x+1)(x-1)=2$\sqrt{2}$x.
分析 (1)方程左边因式分解后利用因式分解法求解方程即可;
(2)将一元二次方程转化为一般形式后利用公式法求解即可.
解答 解:(1)方程左边因式分解得:(x-6)(x+1)=0,
即:x-6=0或x+1=0,
解得:x1=6,x2=-1;
(2)方程左边展开得:x2-1=2$\sqrt{2}$x,
移项得:x2-2$\sqrt{2}$x-1=0,
解得:x=$\frac{2\sqrt{2}±\sqrt{12}}{2}$,
即:x1=$\sqrt{2}$+$\sqrt{3}$,x2=$\sqrt{2}$-$\sqrt{3}$.
点评 本题考查了因式分解法和公式法解一元二次方程的知识,解题的关键是能够正确的判断并采用最为合理的方法因式分解,难度不大.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
3.多项式3xy-5x2y+y-1的次数、项数、最高次项的系数分别是( )
| A. | 2,4,3 | B. | 3,4,-5 | C. | 3,4,5 | D. | 2,4,-5 |
1.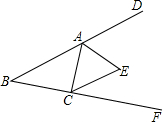 如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E.则∠AEC的度数为( )
如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E.则∠AEC的度数为( )
 如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E.则∠AEC的度数为( )
如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E.则∠AEC的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
8.下列图形中是正方体展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
3.下列计算正确的是( )
| A. | -5-5=0 | B. | -1+1=0 | C. | -3÷$\frac{1}{3}$=-1 | D. | 43=12 |