题目内容
20. 如图,点A是反比例函数y=$\frac{2}{x}$(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-$\frac{3}{x}$的图象于点B,以AB为边作□ABCD,其中C、D在x轴上,则S□ABCD为( )
如图,点A是反比例函数y=$\frac{2}{x}$(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-$\frac{3}{x}$的图象于点B,以AB为边作□ABCD,其中C、D在x轴上,则S□ABCD为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 设A的纵坐标是b,则B的纵坐标也是b,即可求得A、B的横坐标,则AB的长度即可求得,然后利用平行四边形的面积公式即可求解.
解答 解:设A的纵坐标是b,则B的纵坐标也是b.
把y=b代入y=$\frac{2}{x}$得,b=$\frac{2}{x}$,则x=$\frac{2}{b}$,即A的横坐标是$\frac{2}{b}$,;
同理可得:B的横坐标是:-$\frac{3}{b}$.
则AB=$\frac{2}{b}$-(-$\frac{3}{b}$)=$\frac{5}{b}$.
则S□ABCD=$\frac{5}{b}$×b=5.
故选D.
点评 本题考查了是反比例函数与平行四边形的综合题,理解A、B的纵坐标是同一个值,表示出AB的长度是关键.

练习册系列答案
相关题目
15.如果|-a|=a,则下列a的取值不能使这个式子成立的是( )
| A. | 0 | B. | 1 | C. | 2 | D. | a取任何负数 |
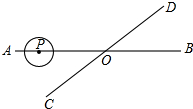 如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的圆P的圆心在直线AB上,且与点O的距离为10cm,如果⊙P以2cm∕s的速度,沿由A向B的方向移动,那么4或6秒钟后⊙P与直线CD相切.
如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的圆P的圆心在直线AB上,且与点O的距离为10cm,如果⊙P以2cm∕s的速度,沿由A向B的方向移动,那么4或6秒钟后⊙P与直线CD相切.

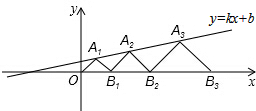 如图,在平面直角坐标系中,点A1、A2、A3…和点B1、B2、B3…分别在直线y=kx+b和x轴上,△OA1B1、△B1A2B2、△B2A3B3…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么A3的坐标是($\frac{29}{5}$,$\frac{9}{4}$),A2015的坐标是(5×($\frac{3}{2}$)2014-4,($\frac{3}{2}$)2014).
如图,在平面直角坐标系中,点A1、A2、A3…和点B1、B2、B3…分别在直线y=kx+b和x轴上,△OA1B1、△B1A2B2、△B2A3B3…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么A3的坐标是($\frac{29}{5}$,$\frac{9}{4}$),A2015的坐标是(5×($\frac{3}{2}$)2014-4,($\frac{3}{2}$)2014).