题目内容
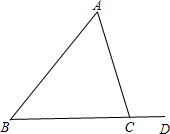如图所示，∠ACD=115°，∠B=55°，则∠A=60°
60°
，∠ACB=65°
65°
．分析：根据三角形的外角性质可得：∠A+∠B=∠ACD，求出∠A度数，然后根据∠ACB和∠ACD互为邻补角即可求得∠ACB的度数．
解答：解：∵∠ACD为△ABC的外角，
∴∠ACD=∠A+∠B，
则∠B=115°-55°=60°，
又∠ACB和∠ACD互为邻补角，
∴∠ACB=180°-∠ACD=180°-115°=65°．
故答案为：60°，65°．
∴∠ACD=∠A+∠B，
则∠B=115°-55°=60°，
又∠ACB和∠ACD互为邻补角，
∴∠ACB=180°-∠ACD=180°-115°=65°．
故答案为：60°，65°．
点评：本题考查了三角形的外角性质，属于基础题，解答本题的关键是熟练掌握三角形的一个外角等于和它不相邻的两个内角的和．
练习册系列答案
相关题目
1、如图所示，△ACD≌△BDC，且点C和点D是对应点，BC=3，BD=4，那么AD=
如图所示，△ACD和△BCE都是等边三角形，△DCB经过旋转后得到△ACE．
如图所示，∠ACD是△ABC的一个外角，
如图所示，∠ACD是△ABC的外角，CE平分∠ACD，F是CA延长线上的一点，FG∥EC交AB于点G，若∠1=62°，∠B=40°，求∠2的度数．