题目内容
18.(1)如图甲,在水塔O的东北方向32m处有一抽水站A.在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,求水管AB的长.(2)如图乙,在△ABC中,D是BC边上的点.已知AB=13,AD=12,AC=15,BD=5,求DC的长.
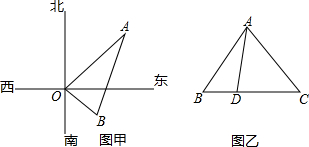
分析 (1)根据题意得出:∠AOB=90°,再利用勾股定理得出AB的长;
(2)利用勾股定理的逆定理得出∠ADB=∠ADC=90°,再利用勾股定理得出答案.
解答 解:(1)由题意可得:∠AOB=90°,
在Rt△AOB中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{3{2}^{2}+2{4}^{2}}$=40(m),
答:水管AB的长为40m;
(2)∵AB=13,AD=12,BD=5,
∴AB2=132=169,BD2=52=25,DA2=122=144,
∴AB2=BD2+DA2,
∴∠ADB=∠ADC=90°,
在Rt△ADC中,又AC=15,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{1{5}^{2}-1{2}^{2}}$=9.
点评 此题主要考查了勾股定理以及其逆定理,得出∠ADB=∠ADC=90°是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列描述一次函数y=-2x+5的图象及性质错误的是( )
| A. | y随x的增大而减小 | B. | 直线经过第一、二、四象限 | ||
| C. | 当x>0时y<5 | D. | 直线与x轴交点坐标是(0,5) |
3.下列调查不适合全面调查而适合抽样调查的是( )
①了解2015年5月份冷饮市场上冰淇淋的质量情况;
②了解全国网迷少年的性格情况;
③环保部门了解2015年5月份黄河某段水域的水质量情况;
④了解全班同学本周末参加社区活动的时间.
①了解2015年5月份冷饮市场上冰淇淋的质量情况;
②了解全国网迷少年的性格情况;
③环保部门了解2015年5月份黄河某段水域的水质量情况;
④了解全班同学本周末参加社区活动的时间.
| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③ |
7.如果mn<0,且m<0,则点P(m2,n-m)在( )
| A. | 笫一象限 | B. | 笫二象限 | C. | 笫三象限 | D. | 笫四象限 |
8.下列语句中正确的是( )
| A. | 同位角都相等 | |
| B. | 同一平面内,不相交的两条直线叫做平行线 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 两直线平行,同旁内角相等 |