题目内容
2.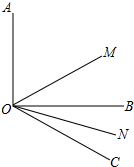 如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为 ( )
如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为 ( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
分析 根据角平分线的定义得到∠MOC=$\frac{1}{2}$∠AOC,∠NOC=$\frac{1}{2}$∠BOC,则∠MON=∠MOC-∠NOC=$\frac{1}{2}$(∠AOC-∠BOC)=$\frac{1}{2}$∠AOB,然后把∠AOB的度数代入计算即可.
解答 解:∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=$\frac{1}{2}$∠AOC,∠NOC=$\frac{1}{2}$∠BOC,
∵∠AOC=∠AOB+∠BOC,
∴∠MON=∠MOC-∠NOC=$\frac{1}{2}$(∠AOB+∠BOC-∠BOC)=$\frac{1}{2}$∠AOB,
∵∠AOB=90°,
∴∠MON=$\frac{1}{2}$×90°=45°.
故选B.
点评 本题考查了角平分线的定义,做这类题时学生总会认为条件不够,其实只要把这些等量关系合并化简即可求出角的度数,所以学生做题时有是不要急于计算,而是要先化简后再合并,属于基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
2.在一个有12万人的小镇,随机调查了3000人,其中500人看某电视台的早间新闻.那么,在该小镇随便问一个人,他看该电视台早间新闻的概率大约是( )
| A. | $\frac{1}{240}$ | B. | $\frac{1}{40}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
7.已知数549039用四舍五入法保留两个有效数字是5.5×105,则所得近似数精确到( )
| A. | 十位 | B. | 千位 | C. | 万位 | D. | 百位 |
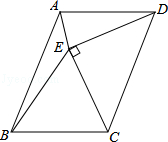 如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是135°.
如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是135°.