Question

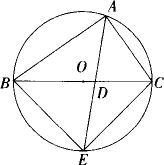
如下图，△ABC内接于⊙O，AB是直径，BC=4，AC=3，CD平分∠ACB，则弦AD长为

[　　]

A．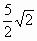

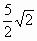
B．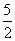

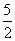
C．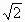

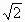
D．3

Answer 1

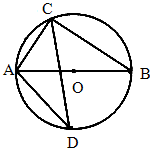
答案：A
解析：

连接BD．∵AB是⊙O的直径，∴∠ACB=∠ADB=90°．在Rt△ABC中，．∵∠ACD=∠BCD，∴AD=BD． 设AD=BD=x，则有勾股定理，得． ∴，(舍)，即．

提示：

易得△ABC是直角三角形，利用勾股定理可以求得AB．∠ACB是圆周角，CD将其平分后的两个角所对的弦相等，则在Rt△ABD中可以求得AD．