Question

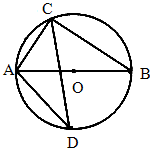
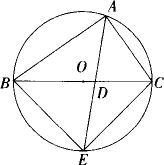
如下图，△ABC内接于⊙O，∠BAC的平分线交BC于D，交⊙O于E，若∠BAC＝90°，则AE²＝2S_{四边形ABEC}．

Answer 1

答案：
解析：

证明：∵AE平分∠BAC， 　　根据上述定理，有 　　AB·AC＝AD·AE．　　① 　　∴∠BAC＝90°， 　　∴∠EBC＝∠CAE＝∠BAE＝45° 　　又∠BED＝∠AEB， 　　∴△BED∽△AEB， 　　∴， 　　∴BE2＝DE·AE．　　　② 　　①＋②得AD·AE＋DE·AE＝AB·AC＋BE2， 　　AE(AD＋DE)＝AB·AC＋BE2 　　AE2＝AB·AC＋BE2． 　　∵∠BEC＝180°－∠BAC＝90°，且BE＝EC． 　　∴BE2＝BE·EC＝2S△BEC， 　　又AB·AC＝2S△ABC， 　　∴AB·AC＋BE2＝2(S△ABC＋S△BEC)＝2S四边形ABEC． 　　∴AE2＝2S四边形ABEC．