题目内容
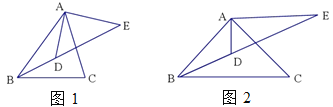
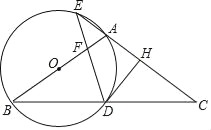
【题目】如图,平行四边形纸片ABCD的边AB,BC的长分别是10cm和7.5cm,将其四个角向内对折后,点B与点C重合于点C',点A与点D重合于点A′.四条折痕围成一个“信封四边形”EHFG,其顶点分别在平行四边形ABCD的四条边上,则EF=__cm.
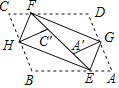
【答案】10.
【解析】
先根据有三个角是直角的四边形是矩形证明四边形EHFG是矩形,再证明△FCH≌△EAG,可得CF=AE=FC',可知EF=AB,即可得结论.
如图中,
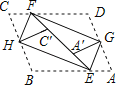
由翻折可知:∠CHF=∠FHC',∠BHE=∠EHC',
∴∠FHE=∠FHC'+∠EHC'![]() (∠CHC'+∠BHC')=90°,
(∠CHC'+∠BHC')=90°,
同法可证:∠HFG=∠GEH=90°,
∴四边形EHFG是矩形.
∴FH=EG,FH∥EG,
∴∠HFC'=∠FEG,
∵∠CFH=∠HFC',∠AEG=∠GEA',
∴∠CFH=∠AEG,
∵四边形ABCD是平行四边形,
∴∠C=∠A,BC=AD,
由翻折得:CH=C'H=BH![]() BC,AG=A'G=DG
BC,AG=A'G=DG![]() AD,
AD,
∴CH=AG,
∴△HCF≌△GAE(AAS),
∴CF=AE,
∴EF=FC'+EC'=AE+BE=AB=10cm,
故答案为:10.

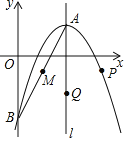
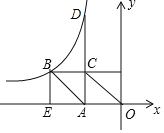
【题目】如图,已知反比例函数y=![]() (x<0)的图象经过OABC的顶点B,点A在x轴上,AC⊥x轴交反比例函数图象于点D,BE⊥x轴于点E,则BE:AD=( )
(x<0)的图象经过OABC的顶点B,点A在x轴上,AC⊥x轴交反比例函数图象于点D,BE⊥x轴于点E,则BE:AD=( )
A. 1:2B. 1:![]() C. 1:3D. 1:
C. 1:3D. 1:![]()
【题目】陈老师对他所教的九(1)、九(2)两个班级的学生进行了一次检测,批阅后对最后一道试题的得分情况进行了归类统计(各类别的得分如下表),并绘制了如图所示的每班各类别得分人数的条形统计图(不完整).
各类别的得分表
得分 | 类别 |
|
|
|
|
|
|
|
|
已知两个班一共有![]() 的学生得到两个正确答案,解答完全正确,九(1)班学生这道试题的平均得分为
的学生得到两个正确答案,解答完全正确,九(1)班学生这道试题的平均得分为![]() 分.请解决如下问题:
分.请解决如下问题:
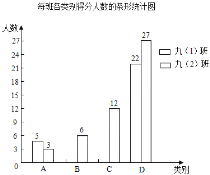
(1)九(2)班学生得分的中位数是 ______;
(2)九(1)班学生中这道试题作答情况属于![]() 类和
类和![]() 类的人数各是多少?
类的人数各是多少?