题目内容
【题目】将在同一平面内如图放置的两块三角板绕公共顶点A旋转,连接BC,DE.探究S△ABC与S△ADC的比是否为定值.
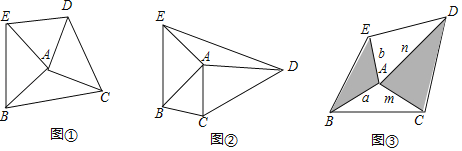
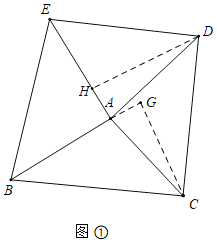
(1)两块三角板是完全相同的等腰直角三角板时,S△ABC:S△ADE是否为定值?如果是,求出此定值,如果不是,说明理由.(图①)
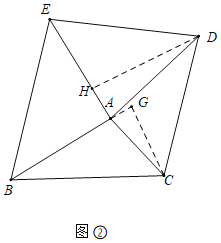
(2)一块是等腰直角三角板,另一块是含有30°角的直角三角板时,S△ABC:S△ADE是否为定值?如果是,求出此定值,如果不是,说明理由.(图②)
(3)两块三角板中,∠BAE+∠CAD=180°,AB=a,AE=b,AC=m,AD=n(a,b,m,n为常数),S△ABC:S△ADE是否为定值?如果是,用含a,b,m,n的式子表示此定值(直接写出结论,不写推理过程),如果不是,说明理由.(图③)
【答案】(1)结论:S△ABC:S△ADE=1,为定值.理由见解析;(2)S△ABC:S△ADE=![]() ,为定值,理由见解析;(3)S△ABC:S△ADE=
,为定值,理由见解析;(3)S△ABC:S△ADE=![]() ,为定值.理由见解析.
,为定值.理由见解析.
【解析】
(1)结论:S△ABC:S△ADE=定值.如图1中,作DH⊥AE于H,CG⊥BA交BA的延长线于G.首先证明∠DAE=∠CAG,利用三角形的面积公式计算即可.
(2)结论:S△ABC:S△ADE=定值.如图1中,作DH⊥AE于H,CG⊥BA交BA的延长线于G.首先证明∠DAE=∠CAG,利用三角形的面积公式计算即可.
(3)结论:S△ABC:S△ADE=定值.如图1中,作DH⊥AE于H,CG⊥BA交BA的延长线于G.首先证明∠DAE=∠CAG,利用三角形的面积公式计算即可.
(1)结论:S△ABC:S△ADE=定值.
理由:如图1中,作DH⊥AE于H,CG⊥BA交BA的延长线于G.
∵∠BAE=∠CAD=90°,
∴∠BAC+∠EAD=180°,∠BAC+∠CAG=180°,
∴∠DAE=∠CAG,
∵AB=AE=AD=AC,
∴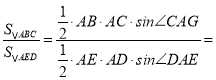 1.
1.
(2)如图2中,S△ABC:S△ADE=定值.
理由:如图1中,作DH⊥AE于H,CG⊥BA交BA的延长线于G.
不妨设∠ADC=30°,则AD![]() AC,AE=AB,
AC,AE=AB,
∵∠BAE=∠CAD=90°,
∴∠BAC+∠EAD=180°,∠BAC+∠CAG=180°,
∴∠DAE=∠CAG,
∴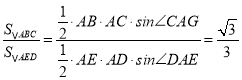 .
.
(3)如图3中,如图2中,S△ABC:S△ADE=定值.
理由:如图1中,作DH⊥AE于H,CG⊥BA交BA的延长线于G.
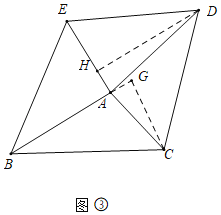
∵∠BAE=∠CAD=90°,
∴∠BAC+∠EAD=180°,∠BAC+∠CAG=180°,
∴∠DAE=∠CAG,
∵AB=a,AE=b,AC=m,AD=n
∴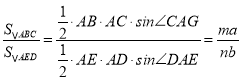 .
.

 阅读快车系列答案
阅读快车系列答案【题目】如图,菱形![]() 的顶点
的顶点![]() 、
、![]() 在
在![]() 轴上(
轴上(![]() 在
在![]() 的左侧),顶点
的左侧),顶点![]() 、
、![]() 在
在![]() 轴上方,对角线
轴上方,对角线![]() 的长是
的长是![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 在菱形
在菱形![]() 的边上运动.当点
的边上运动.当点![]() 到
到![]() 所在直线的距离取得最大值时,点
所在直线的距离取得最大值时,点![]() 恰好落在
恰好落在![]() 的中点处,则菱形
的中点处,则菱形![]() 的边长等于( )
的边长等于( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】为了增强学生的安全意识,某校组织了一次全校2500名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了100份考卷进行分析统计,发现考试成绩(![]() 分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.请根据图表提供的信息,解答下列问题:
分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.请根据图表提供的信息,解答下列问题:
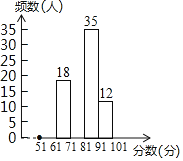
分数段(分) | 频数(人) | 频率 |
|
| 0.1 |
| 18 | 0.18 |
|
|
|
| 35 | 0.35 |
| 12 | 0.12 |
合计 | 100 | 1 |
(1)填空:![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)将频数分布直方图补充完整;
(3)该校对考试成绩为![]() 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为1:3:6,请你估算全校获得二等奖的学生人数.
的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为1:3:6,请你估算全校获得二等奖的学生人数.