题目内容
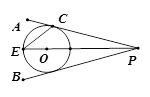
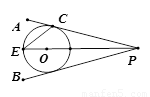
如图,点O在∠APB的平分线上,⊙O与PA边相切于点C,
(1)求证:PB是⊙O的切线;
(2)PO的延长线交⊙O于E,EA⊥PA于A.设PE交⊙O于另一点G,AE交⊙O于点F,连接FG,若⊙O的半径是3,=.
①求弦CE的长;②求的值.

(1)证明:连接OC,过点O作OD⊥PB于点D,
∵PA切⊙O于点C, ∴OC⊥PA
∵PO平分∠BPA,
∴OC=OD
∴PB是⊙O的切线; (2)①连接CG,
∵EA⊥PA于A∴∠APC+∠ECA=90°
∵OC⊥PA, ∴∠OCE+∠EAC=90°
∴∠OCE=∠CEA
∵OC=OE, ∴∠OCE=∠OEC
∴∠AEC=∠CEG
∵EG为⊙O的直径,∴∠ECG=90°
∵tan∠AEC=![]() , ∴tan∠CEG=
, ∴tan∠CEG=![]()
设CG=![]() ,则CE=
,则CE=![]() ,∵⊙O的半径为3,∴直径EG=6
,∵⊙O的半径为3,∴直径EG=6
∴![]()
解之得,![]() (不合题意,舍去)
(不合题意,舍去)
∴![]()
②∵OC⊥PA, ∴∠OCG+∠PCG=90°
∵OC=OE, ∴∠OCG=∠OGC
而∠ECG=90°,∴∠OGC+CEG=90°
∴∠PCG=∠CEG
∵∠EPC=∠CPG
∴△PCG∽△PEC ∴![]()
设PG=![]() 则PC=
则PC=![]() ,在Rt△POC中,OG=OC=3
,在Rt△POC中,OG=OC=3
用勾股定理易得![]()
∵∠GFE=∠PAE=90°∴GF∥PA
∴△EGF∽△EPA
∴![]()


练习册系列答案
相关题目
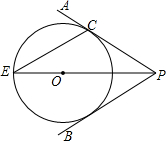 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
如图,点O在∠APB的平分线上,⊙O与PA相切于点C.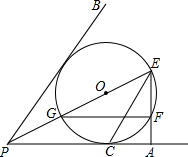 (2012•湖北模拟)如图,点O在∠APB的平分线上,⊙O与PA边相切于点C,
(2012•湖北模拟)如图,点O在∠APB的平分线上,⊙O与PA边相切于点C,